기계학습이란?
machine learning
경험을 통해 나중에 유사하거나 같은 일:task를 더 효율적으로 처리할 수 있도록 시스템의 구조나 파라미터를 바꾸는 것이다. 컴퓨터가 데이터로부터 특정 문제해결을 위한 지식을 자동으로 추출하여 사용할 수 있게 하는 기술이다.
연역적 학습 : deductive learning
deductive inference를 통한 학습
귀납적 학습 : inductive learning
사례들을 일반화하여 패턴이나 모델을 추출함
=> 일반적인 기계학습의 대상으로 학습 데이터를 잘 설명할 수 있는 패턴을 찾는 것이다.
오컴의 면도날 : Occam's rezor => 가능하면 학습 결과를 간단한 형태로 표현하는 것이 좋음
=> 아주 복잡하며 99%의 성능인 모델보다는 95%의 성능을 내면서도 보다 간단한 모델이 좋음 : like 과적합
기계학습의 종류
- 지도학습 : supervised learning
입력:문제과 출력:답의 데이터를 모두 가지고 있을 때, 새로운 입력에 대한 출력을 결정하는 패턴 학습
- 비지도 학습 : unsupervised learning
출력에 대한 정보가 없는, 즉 답을 모르는 데이터들로부터 필요한 패턴 추출 (like 자율학습)
- 반지도 학습 : semisupervised learning
일부 학습 데이터만 출력값이 주어진 상태에서 일반화된 패턴 추출
- 강화학습 : reinforcement learning
출력에 대한 정확한 정보를 제공하지는 않지만 평가 정보:rewaed는 주어질 때, 각 상태에서의 행동을 결정함
기계학습의 여러 task
분류 / 회귀 / 군집화 / 밀도 추정 / 차원 축소 / 이상치탐지 / 반지도 학습
분류
(과적합 문제, 학습 데이터가 적은 문제, 불균형 데이터 문제, 이진 분류기 성능 평가)
지도학습 분류
=> 주어진 입력,출력에 대한 데이터를 학습 데이터로 사용하여 새로운 입력에 대한 결과를 결정할 수 있도록 하는 방법(적절한 함수) 찾기
- 분류 : 출력이 정해진 부류(class, category) 중 하나로 결정
- 회귀 : regression, 출력이 연속인 영역의 값(continuous domain) 결정
classification
데이터들을 몇 개의 부류로 대응시키는 문제 : decision boundary
분류 문제의 학습으로는 학습 데이터를 잘 분류해낼 수 있는 함수를 찾는 것이다 => 함수의 형태는 수학적 함수이거나 규칙
classifier : 학습된 함수를 이용해 데이터를 분류하는 프로그램
분류기 알고리즘
- decision tree algorithm
- K-nearest neighbor : KNN algorithm
- multi perceprton neural network
- deep learning algorithm
- support vector machine : SNM
- AdaBoost
- random forest
- probabilistic graphical model
이상적 분류기는 학습에 사용되지 않은 데이터에 대해 정확한 분류를 하는 것이다. 즉 일반화 능력이 중요하다
data 종류
training data
: 분류기 학습에 사용하는 데이터 집합으로 학습 데이터는 많을 수록 유리하다
test data
: 학습된 모델의 성능을 평가할 때 사용되는 데이터 집합으로 학습에 사용되지 않은 데이터여야함
validation data
: 학습 과정에서 학습을 중단할 시점을 결정하기 위해 사용하는 데이터 집합
overfitting, underfitting
과적합은 학습 데이터를 과도하게 학습하여 학습되지 않은 데이터를 test하였을 때, 성능이 좋지 않은 것
부적합은 학습 데이터를 충분히 학습하지 않은 상태이다
=> 과적합 개선 방법이라 하면 학습을 진행할 수록 오류가 개선되는 경향이 있다. 하지만 여기서 지나치게 학습이 진행되면 과적합이 발생하게 되므로 validation 데이터에 대해 학습 중간 과정에서 성능 평가를 진행한다. 이때 검증 데이터에 대한 오류가 감소하다가 증가하는 시점에 학습을 중단하면 된다.
분류기 성능 평가
- accuracy : 얼마나 정확하게 분류하는가, (옳게 분류한 데이터 수 / 전체 데이터 수)로 테스트 데이터에 대한 정확도를 분류기의 정확도로 사용함
정확도가 높기 위해서는 많은 학습 데이터를 사용하는 것이 유리하며 학습 데이터와 테스트 데이터는 겹치지 않도록 해야한다
데이터가 부족한 경우, 별도의 테스트 데이터를 확보하는 것은 비효율적이다 오히려 가능하면 많은 데이터를 학습에 사용하며 성능을 평가하는 방법이 필요하다
=> K-fold cross validation
전체 데이터를 k등분한 후 각 등분을 한 번씩 테스트 데이터로 사용하며 성능 평가를 하고 최종 성능으로 평균값을 선택함

데이터가 불균형인 경우, imbalanced data
특정 class에 속하는 학습 데이터의 개수가 전체의 99%인 경우, 오히려 해당 클래스로만 분류를 하더라도 성능은 99%
=> 가중치를 고려한 정확도 척도 사용
=> 많은 학습 데이터를 갖는 부류에서 재표본 추출 : re-sampling
=> 적은 학습 데이터를 갖는 부류에 대해 인공적 데이터 생성 : SMOTH 알고리즘
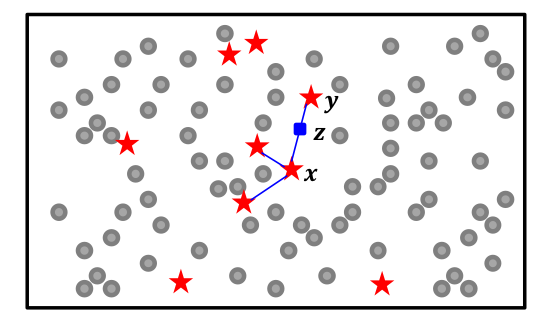
SMOTE : synthetic minority over-sampling technique algorithm
빈도가 낮은 부류의 학습 데이터를 인공적으로 만들어내는 방법이다.
- 임의로 낮은 빈도 부류의 학습 데이터 x를 선택한다
- x의 k-근접이웃인 같은 부류의 데이터를 선택함
- k-근접 이웃 중 무작위로 하나 y를 선택함
- x,y를 연결하는 직선 상의 무작위 위치에 새로운 데이터를 생성함
binary classifier 성능 평가

sensitivity = recall = true positive rate (민감도=재현율=진양성율)
TP/(TP+FN)
=> 실제 양성 중 예측도 양성인 것
specificity = true negative rate (특이도=진음성율)
TN/(FP+TN)
=> 실제 음성 중 예측도 음성인 것
precision (정밀도)
TP/(TP+FP)
=> 예측 양성 중 실제 양성인 것
음성 예측도
TN/(TN+FN)
=> 예측 음성 중 실제 음성인 것
위양성율
FP/(FP+TN) = (1-특이도)
=> 실제로 음성인데 양성으로 예측된 것
위발견율
FP/(TP+FP) = (1-정밀도)
=> 양성으로 예측된 것 중 실제로는 음성인 것
정확도
(TP+TN)/(TP+FP+TN+FN)
F1-score : f1 측도
2(정밀도)(재현율)/(정밀도+재현율)
ROC:receiver operating characteristic curve 곡선
=> 부류 판정 임계값에 따른 위양성율, 민감도 그래프
AUC : area under the curve
=> ROC 곡선에서 곡선 아래 부분 면적으로 클 수록 바람직하다.
AUC-ROC 곡선
다양한 임계값에서 모델의 분류 성능에 대한 측정 그래프
-ROC는 모든 임계값에서 분류 모델의 성능을 보여주는 그래프
-AUC는 ROC곡선의 아래 영역으로 AUC가 높으면 모델의 클래스 구별 성능이 뛰어남을 의미
이 곡선은 정상인 및 환자 클래스 구분 모델의 성능 평가로 흔하게 사용된다.

회귀 : regression
학습 데이터에 부합되는 출력값이 실수인 함수를 찾는 문제
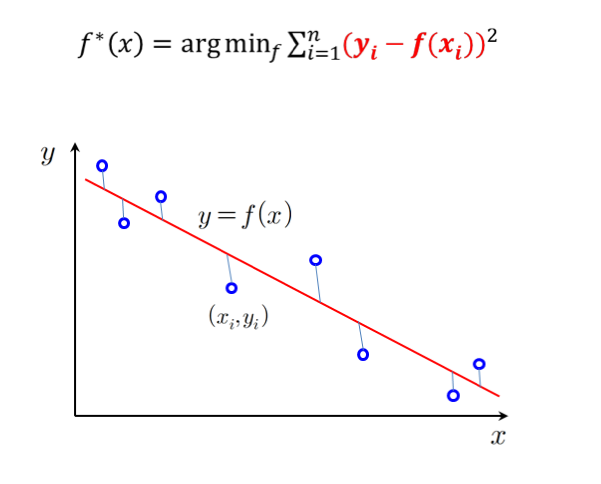
오차 : 실제값 - 예측값
테스트 데이터들에 대한 오차^2의 평균이나 평균의 제곱근을 통해 판별한다.


회귀에서의 과적합 대응 방법
-> 모델의 복잡도를 성능 평가에 반영한다, model complexity를 penalty로 부여
= 목적함수 = 오차의 합 + (가중치 * 모델복잡도)
로지스틱 회귀
로지스틱 함수를 이용하여 함수 근사 적용
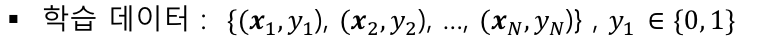


비지도 학습 : unsupervised learning
결과 정보가 없는 데이터들에 대한 특징 패턴 추출
데이터에 잠재한 구조 structure과 계층 구조 hierarchy를 찾아내는 것
숨겨진 사용자 집단을 찾는 것, 문서를 주제에 따라 구조화하는 것, log 정보를 사용해 사용패턴을 찾아내는 것
- clustering : 유사도에 따라 데이터 분할 (segmentation)
- density estimation : 밀도 추정
- dimensionality reduction : 차원 축소
clustering : 유사도에 따라 데이터 분할
- hard clustering, 일반 군집화로 데이터가 하나의 군집에만 소속함 ex) k-means algorithm
- fuzzy clustering, 퍼지 군집화로 데이터가 여러 군집에 부분적으로 소속되며 소속 정도의 합이 1임 ex) fuzzy k-means algorithm
=> 데이터에 내재된 구조를 추정하며 전반적인 구조를 통찰한다.
가설 설정과 이상치 감지를 하며 동일 군집의 데이터를 같은 값으로 표현하여 데이터 압축이 가능하다
데이터 전처리 작업으로도 잘 사용된다.
성능 평가 : 군집 내 분산과 군집 간 거리로 평가된다
작을수록 클수록
density estimation : 밀도 추정
class 별 데이터를 만들어냈을 것으로 추정되는 확률 분포를 찾는 것

=> 각 부류 별 주어진 데이터를 발생시키는 확률을 계산한다.
가장 확률이 높은 부류로 분류를 한다.
- 모수적:parametric 밀도 추정
분포가 특정한 수학적 함수 형태를 가지고 있다고 가정하며 주어진 데이터를 가장 잘 반영하도록 함수의 파라미터를 결정한다.
전형적으로 가우시안 함수:gaussian, 여러개의 가우시안 함수 혼합:mixture of gaussian이 있다.
- 비모수적:nonparametric 밀도 추정
분포에 대한 특정 함수를 가정하지 않고 주어진 데이터를 사용하여 밀도 함수의 형태를 표현한다.
전형적으로 히스토그램:histogram이 있다

dimensionality reduction : 차원 축소
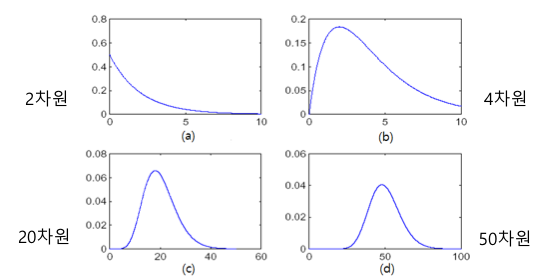
고차원의 데이터를 정보의 손실을 최소화하면서 저차원으로 변환한다
2,3차원으로 변환하여 시각화를 하여 직관적 데이터 분석이 가능하며 curse of dimensionality, 즉 차원의 저주 문제를 완화할 수 있다
- PCA : principle component analysis, 주성분 분석
분산이 큰 소수의 축들을 기준으로 데이터를 projection하여 저차원으로 변환한다.
데이터의 공분산 행렬, covariance matrix에 대한 고유값이 가장 큰 소수의 고유 벡터를 사상 축으로 선택한다.


= 차원의 저주란 차원이 커질수록 거리 분포가 일정해지는 경향이다.

이상치 탐지 : outlier detection
이상치란 다른 데이터와 크게 달라 다른 메커니즘에 의해 생성된 것이 아닌지 의심스러운 데이터로 관심의 대상이 된다
noise란 관측 오류거나 시스템에서 발생하는 무작위적 오차로 관심이 없는 제거 대상이다
이상치 탐지는 신규성 탐지(novelty detection)와 관련이 있다
- 점 이상치 : point outlier로 다른 데이터와 비교하여 차이가 큰 데이터
- 상황적 이상치 : contextual outlier로 상황에 맞지 않는 데이터이다. ex) 여름 25도 정상, 겨울 25도 이상치
- 집단적 이상치 : collective outlier로 여러 데이터르르 모아 보면 비정상으로 보이는 데이터들의 집단이다.


=> 이상치 탐지
- 부정사용감지 시스템 : EFD : fraud detection system
이상한 거래 승인 요청 시 카드 소유자에게 자동으로 경고 메세지 전송
- 침입 탐지 시스템 : IDS : intrusion detection system
네트워크 트래픽을 관찰하여 이상 접근을 식별함
이를 통해 시스템 고장을 진단하며 임상에서 질환 진단 및 모니터링을 할 수 있다
공공 보건에서 유행병을 탐지하며 스포츠 통계학의 특이사건을 감지하거나 관측 오류의 감지 등이 가능하다
반지도 학습 : semi-supervised learning
입력에 대한 결과값이 없는 미분류 데이터를 지도학습에 사용한다
labeled data는 높은 비용, unlabeled data는 낮은 획득 비용이 들기 때문에 분류 경계가 인접한 미분류 데이터를 동일한 집단에 소속하도록 학습한다
같은 군집에 속하는 것은 가능한 한 동일한 분류에 소속하도로 학습한다


'강의 > 인공지능개론' 카테고리의 다른 글
| SVM (0) | 2024.06.07 |
|---|---|
| 기계학습 : 추가 신경망 (1) | 2024.06.05 |
| 기계학습 2.Decision Tree (1) | 2024.06.02 |
| Fuzzy Theory (0) | 2024.04.18 |
| 탐색과 최적화 (0) | 2024.03.13 |

