목차
Decision Tree
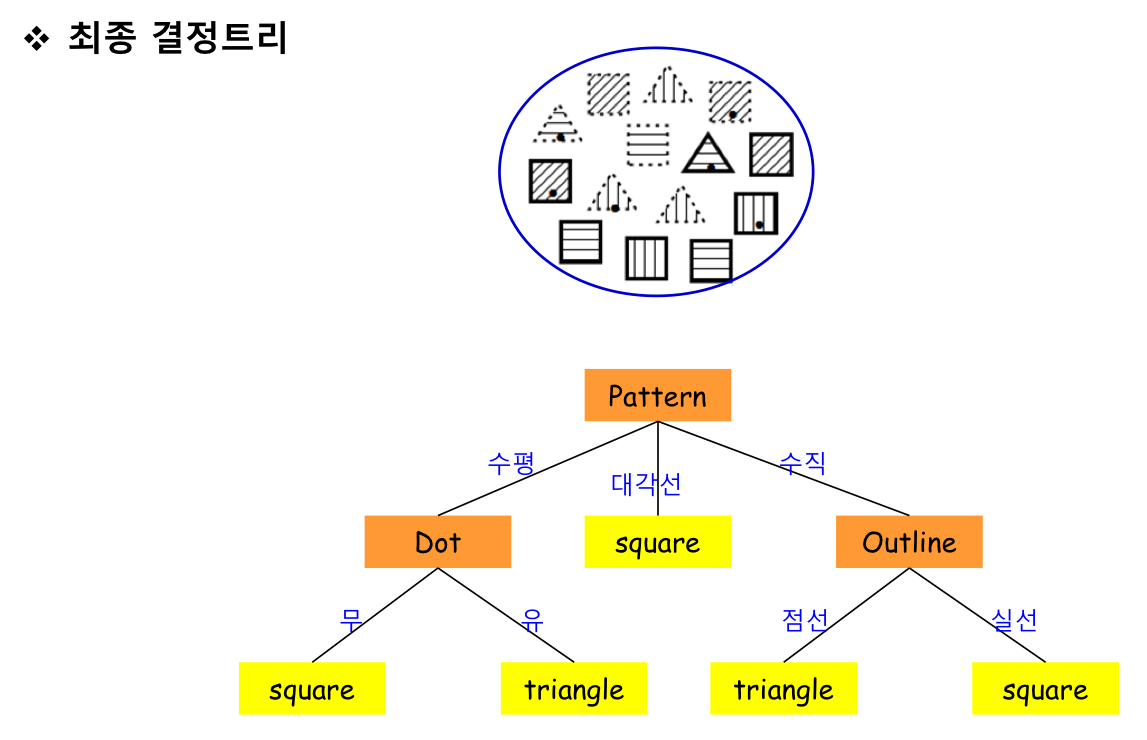
결정트리 형태
결정트리 학습 알고리즘
결정트리를 이용한 회귀
ensemble classifier
k-nearest neighbor, KNN
군집화 알고리즘
naive Bayes classifier
Decision Tree
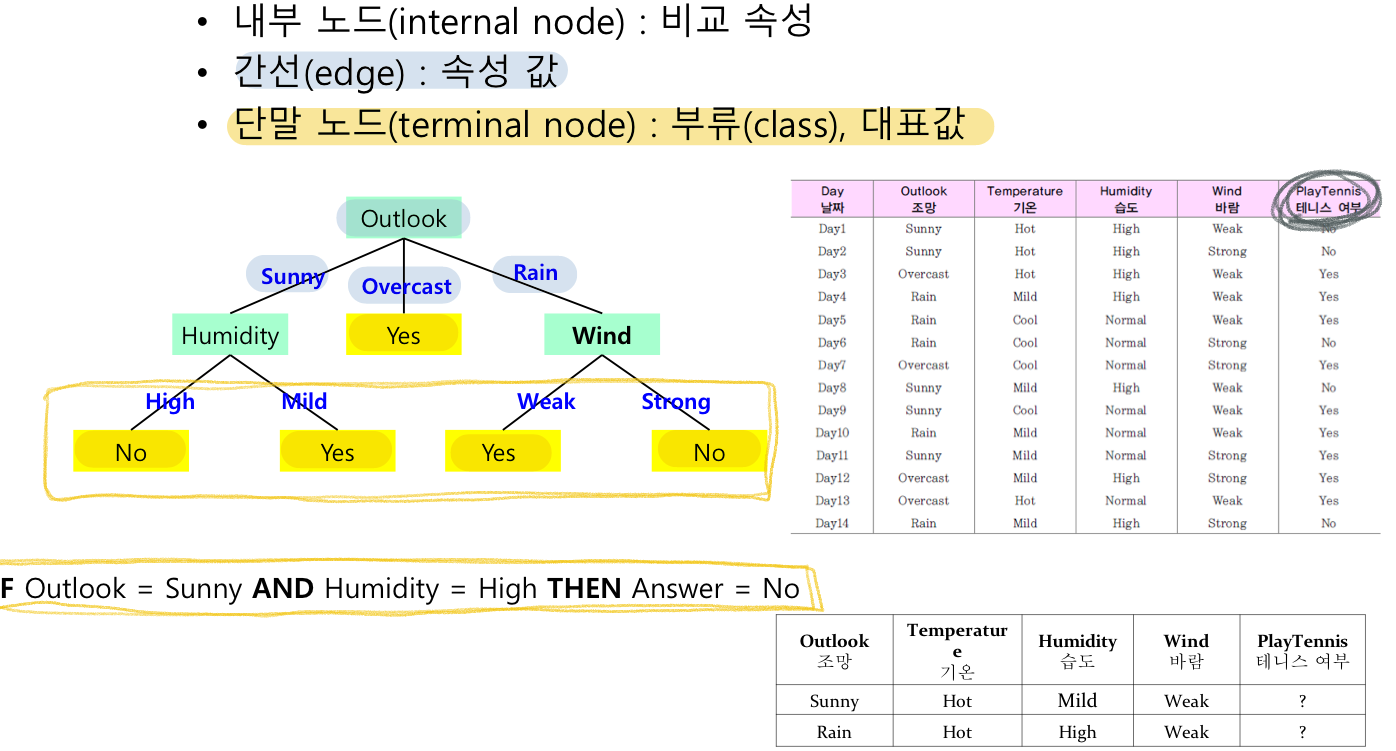
트리의 형태로 의사결정 지식을 표현한 것
결정트리 형태
단말 노드 : class, 대표값
내부 노드 : 노드들 중 단말노드를 제외한 부분으로 비교 속성이라 할 수 있다
간선 : 속성 값
결정트리 학습 알고리즘
Algorithm
- 모든 데이터를 포함한 하나의 노드에서 시작
- 반복적인 노드 분할
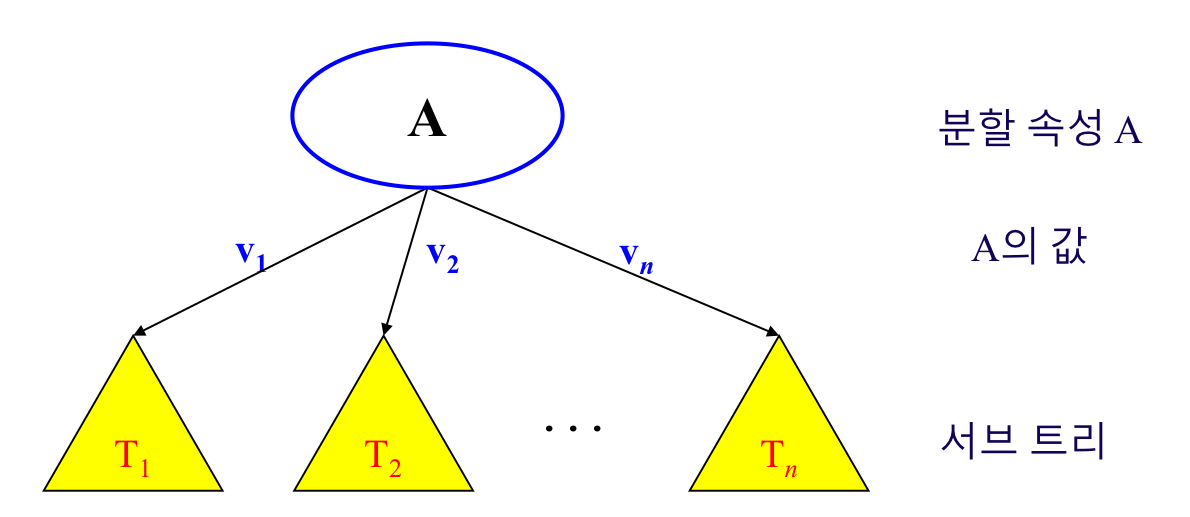
분할 속성을 선택
속성값에 따라 서브 트리 생성
데이터를 속성 값에 따라 분배
=> 이러한 decision tree의 경우, 아주 복잡하여 해당 문제를 세세하게 분류하며 정확도는 99%인 트리와, 비교적 간단하되 정확도는 95%로 약간 떨어지는 트리 중 후자가 더 낫다. 과적합 문제
그렇다면 분할 속성:splitting attribute을 어떻게 결정할 것인가?
어떤 속성을 선택하는 것이 효율적인가?
분할한 결과가 가능하면 동질적:pure인 것으로 만드는 속성을 선택하는 것이 좋다
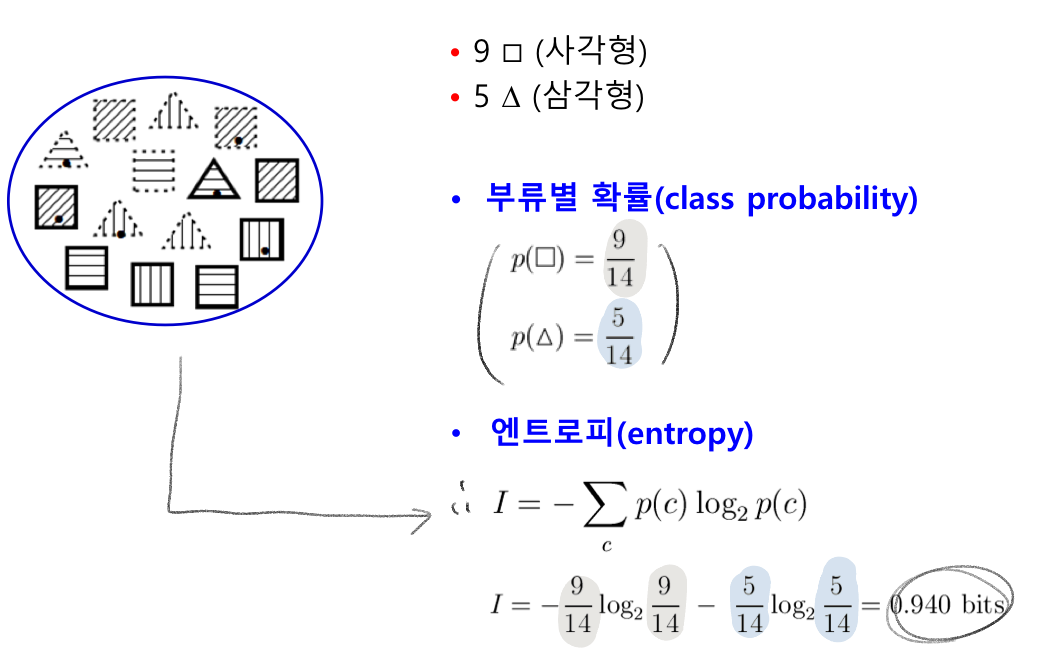
엔트로피 entropy
=> 동질적인 정도를 측정하는 척도이다
정보량 측정 목적의 척도로 엔트로피가 낮다 = 정보량이 확실하게 존재한다 = good

p(c) : 부류 c에 속하는 것의 비율


정보 이득이 높아지는 방향으로 분할해야함
IG = I - Ires
( Ires : 특정한 속성으로 분할한 후의 각 부분집합의 정보량 가중평균 )
= 분할한 후의 정보량 차이
= 정보 이득이 클 수록 우수한 분할 속성

학습 데이터 ex)

결정트리 학습 알고리즘 예시
1) 엔트로피 계산
분류 전 원래 I 계산
2) 속성을 결정해서 분할 후 정보이득 계산 (기존 분류 전 엔트로피와 분류 후 엔트로피 차이 계산)
- 속성의 세부 값들의 엔트로피를 계산하고, 해당 속성의 엔트로피 res 값을 구해서 IG를 비교해야함
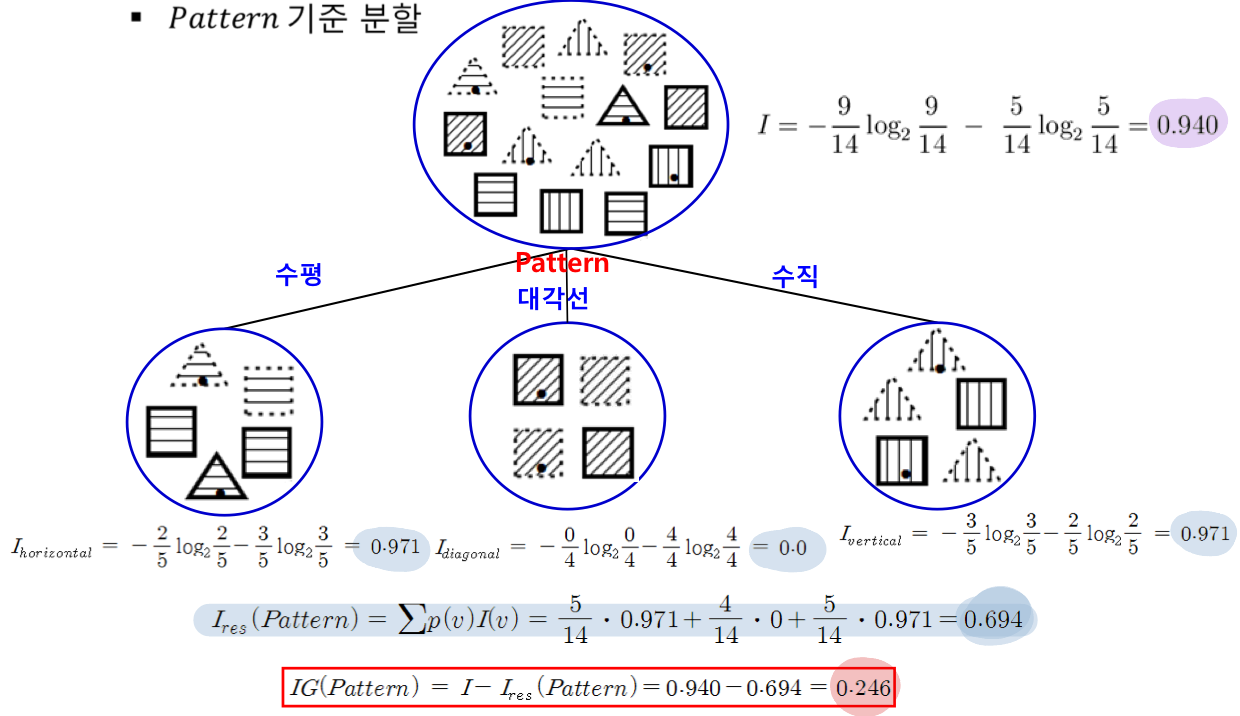


위 과정을 말단 노드(특정 class, 대표값)가 나올 때까지 분류해줘야함


하지만 이러한 정보이득 척도의 단점이라고 한다면!
속성값이 많은 것을 선호한다는 것!=> 분류의 의미가 없는 like 학번이나 이름
속성값이 많으면 데이터 집합을 세부적으로, 많은 부분집합으로 분할하게 됨
이에 대한 개선의 척도는
1. 정보 이득비
2. 지니 지수
** 두 척도 설명 가능해야함
정보이득 비 : information gain ratio
정보이득 척도를 계산한 것
=> 속성값이 많은 속성에 불이익을 줌

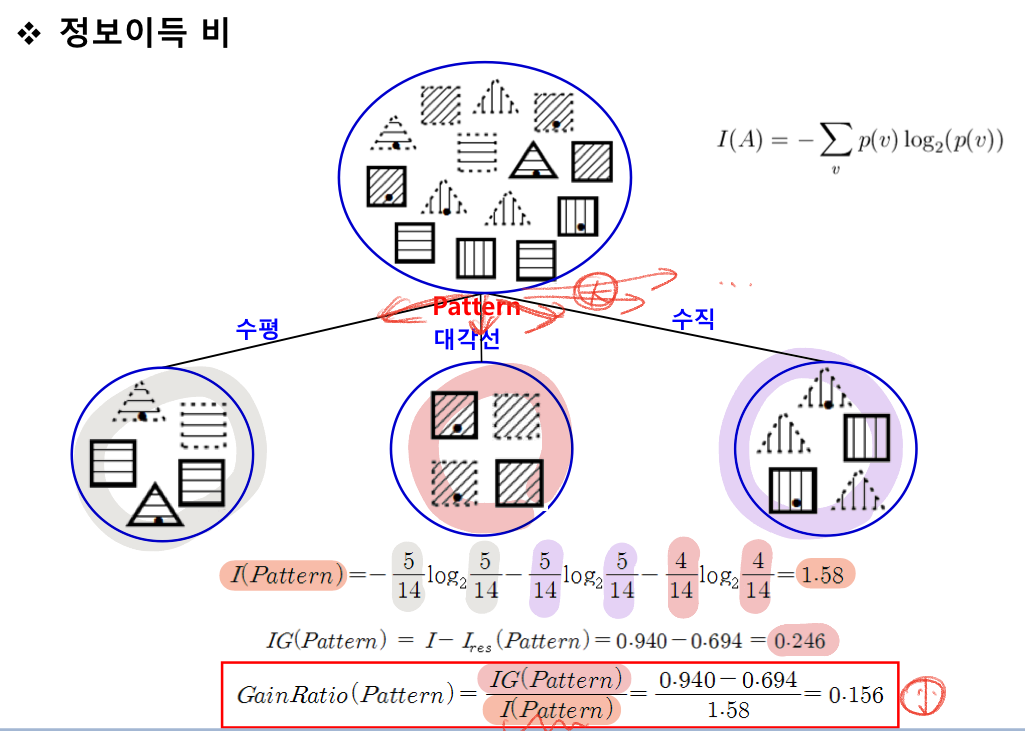
분류 전 엔트로피 구하고
분류 후 각 분류값들의 엔트로피를 사용해서 분류 후 엔트로피 구해서
둘의 차이는 IG를 구함
그 후 분류 후의 엔트로피를 구해서
둘을 나눠주면 정보이득비를 구할 수 있음
지니 지수 : Gini index
데이터 집합에 대한 지니 값
- i,j가 class 라고 한다면


=> 지니 지수를 사용하여 이득값을 계산함

결정트리 알고리즘
- ID3 알고리즘 : 범주형 속성 데이터에 대한 decision tree
- C4.5 알고리즘 : 범주형 속성값, 수치형 속성값을 갖는 데이터에 대한 decision tree
- C5.0 알고리즘 : 4.5 개선
- CART 알고리즘 : 수치형 속성을 갖는 데이터에 적용
결정트리를 이용한 회귀
회귀를 위한 결정트리
=> 출력값이 수치


분류를 위한 결정트리와 차이점이라고 하면 단말 노드가 class값이 아닌 수치값이다
회귀 결정트리의 경우 분할 속성 선택 시, 표준편차 축소인 SDR를 최대로 하는 속성을 선택


ensemble classifier
주어진 학습 데이터 집합에 대해 여러 개의 서로 다른 classifier를 사용하며
이들의 판정 결과를 voting이나 weighted voting을 적용하여 결합한다
- bootstrap : 붓스트랩
주어진 학습 데이터 집합에서 복원 추출하여 다수의 학습 데이터 집합을 만들어냄
- bagging : bootstrap aggregating
붓스트랩을 통해 여러 개의 학습 데이터 집합을 생성
각 학습 데이터 집합별로 classifier를 생성해 학습하고
이들을 voting or weighted voting을 적용하여 최종 판정을 진행함

- boosting
k개 분류기를 순차적으로 만들어가는 앙상블 classifier
=> 분류 정확도에 따라 학습 데이터에 가중치를 변경해가며 분류기를 생성함
=> bagging 보다 성능 더 좋을 수 있음

AdaBoost 알고리즘
N개의 학습 데이터 di에 대한 초기 가중치 wi
-> 학습 오류값 error : 잘못 분류한 학습 데이터의 가중치 합, 값이 0.5 미만인 분류기들만 사용
학습
-> 오류값이 0.5 미만인 분류기가 학습되는 경우
분류기의 신뢰도 알파에 대해
잘못 판정한 학습 데이터 가중치는 크게,
제대로 판정한 학습 데이터의 가중치는 줄여서 적용함
위 가중치 합이 1이 되도록 정규화

k-nearest neighbor, knn
(입력, 결과)가 있는 데이터들이 주어진 상확 속,
새로운 입력에 대한 결과를 추정할 때 결과를 아는 최근접 K개 데이터에 대한 결과정보를 이용하는 방법
질의가 주어지면 k개의 가장 근접한 학습 데이터를 찾기 위해 모든 학습 데이터 간의 거리를 계산해야함
=> 데이터 개수가 많아지면 계산 시간이 증가한다
비교 대상 학습 데이터를 효과적으로 선택하기 위해 indexing, 또는 다양한 자료 구조들을 사용하는 것이 가능
하지만 고차원 데이터에서는 이도 비효율적이다.



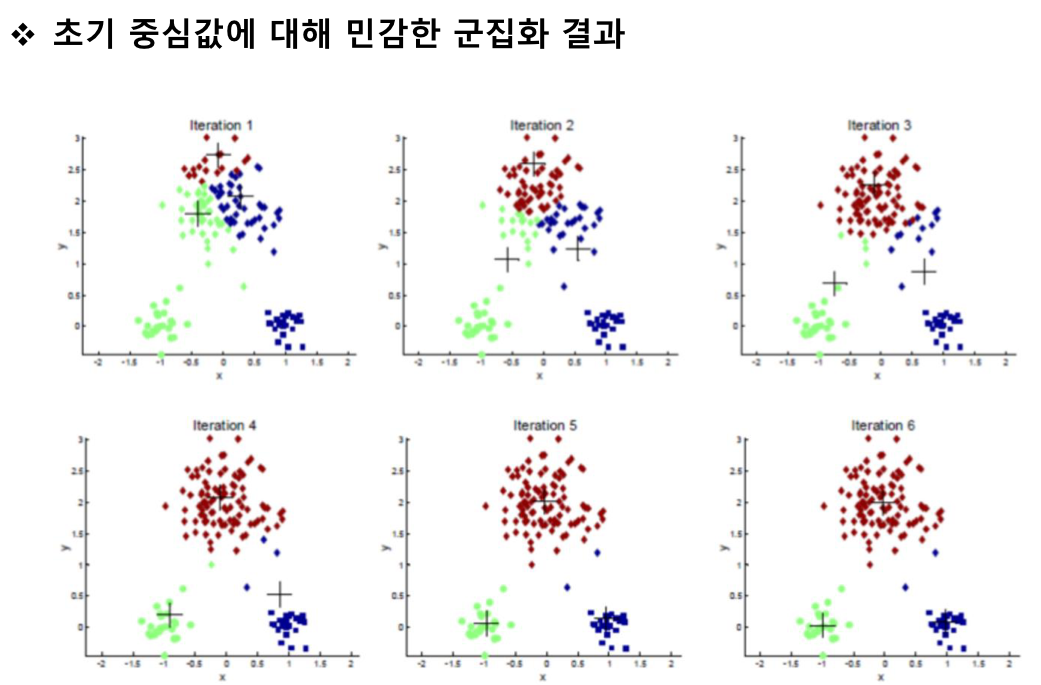
clustering algorithm
군집화 알고리즘
데이터를 유사한 것끼리 분류함
=> 군집 내 유사도는 크게, 군집 외 유사도는 작게
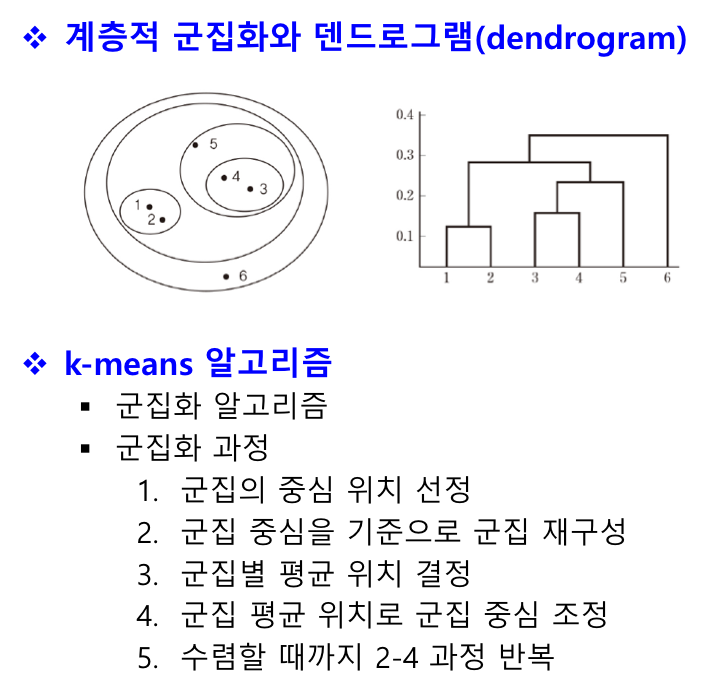
hierarchical clustering
군집화의 결과가 군집들이 계층적인 구조를 갖도록 함
- 병합형 : 각 데이터가 하나의 군집을 구성하는 상태에서 시작하여 가까이 있는 군집끼리 결합하는 과정 반복
- 분리형 : 모든 데이터를 포함한 군집에서 시작해 유사성을 바탕으로 군집을 분리해 계층적 구조를 점차 형성함
partitioning clustering
계층적 구조를 만들지 않고 전체 데이터를 유사한 것들끼리 나누어 묶음
ex) k-means
k-means는 군집화에 사용, knn는 분류, 회귀에 사용

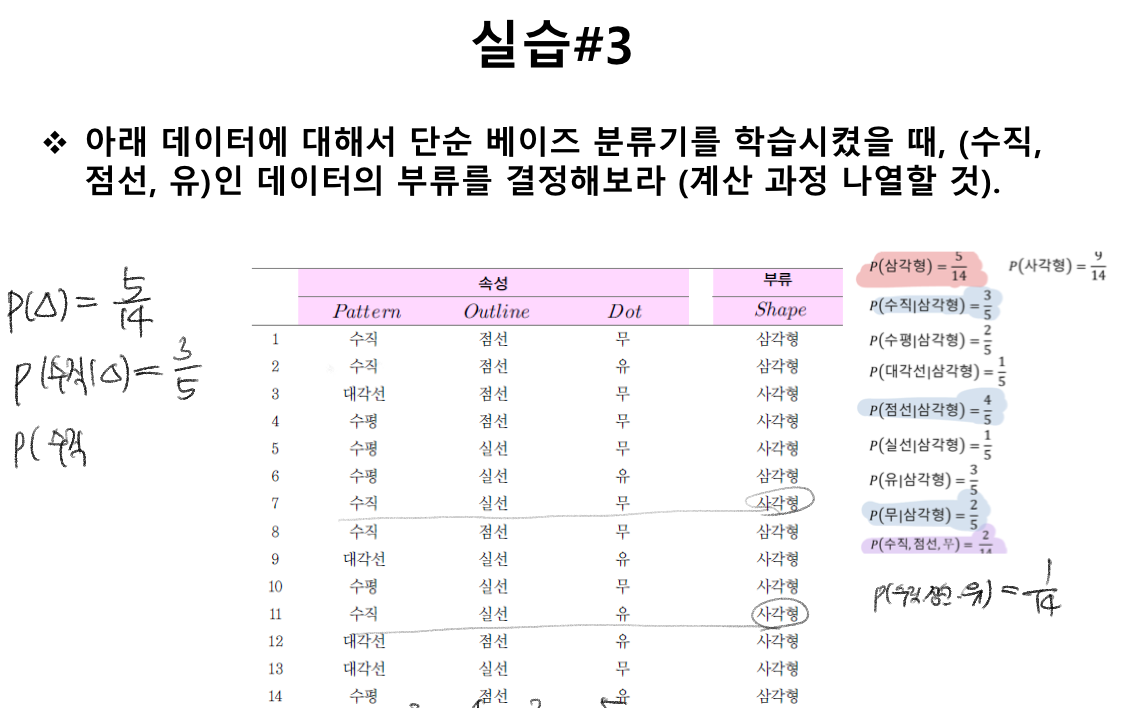
naive Bayes classifier


'강의 > 인공지능개론' 카테고리의 다른 글
| SVM (0) | 2024.06.07 |
|---|---|
| 기계학습 : 추가 신경망 (1) | 2024.06.05 |
| 기계학습 1 (2) | 2024.05.10 |
| Fuzzy Theory (0) | 2024.04.18 |
| 탐색과 최적화 (0) | 2024.03.13 |


