현실적 상황 속 데이터 => 불균형 데이터 분포가 많음 => 원시 데이터의 증강이 목표
DCGAN 등 다양한 GAN이 존재 => 그 중 WGAN, WGAN-GP는 안정적으로 최적화됨
1) 기본 GAN의 알고리즘
2) WGAN-GP를 사용한 검증 방법
3) GAN 효과 test 실험
순으로 정리해보겠음
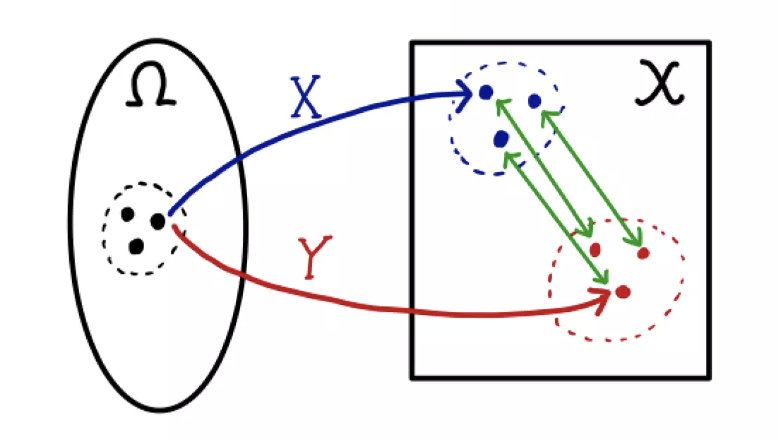
1) Generative Adverserial network
훈련 전략 : minimax 게임
-generator : 가우스, 균일 분포의 noise 분포에서 샘플을 가져와서 기존 실제 데이터와 동일한 데이터 공간으로 mapping
=> 가능한 현실적인 데이터를 만들어내도록 훈련받음
-discriminator : 입력된 가짜(생성된) 데이터와 실제 데이터 구분
=> 생성된 데이터에 속지 않도록 훈련받음
두 모델이 적대적 관계를 가지며 학습진행됨
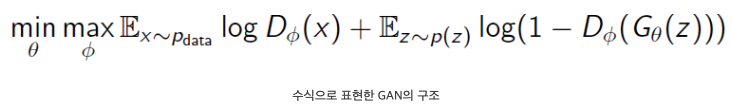
generator : G, G의 parameter : θ / discriminator : D , D의 parameter : ϕ
1 : real data, 0 : fake data, x : real data 분포, z : nosie
discriminator : D(x) => 1로 만들어 real data를 1로 분류 / D(G(z)) => 0으로 만들어 fake data를 0으로 분류
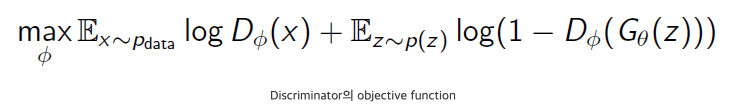
generator : D(G(z)) => 1로 만들어 판별자를 속이려 한다.

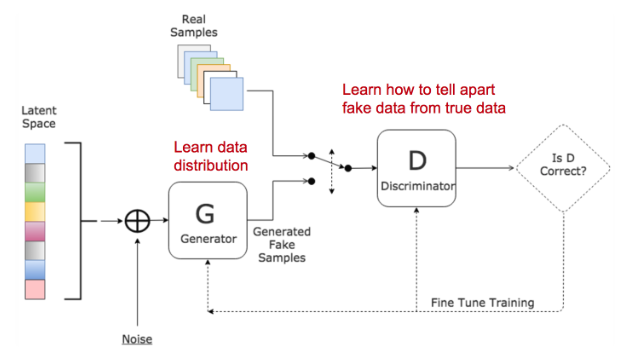
근데 이제 (1) minimax 게임은 원래 불안정함 => Jensen-Shannon 발산
(2) 수렴 문제 존재, 훈련을 언제 멈춰야하는지 모른다.
학습 정도를 알려면 샘플을 직접 확인하여 보는 수밖에 없다.
+ 위 object function을 적용하면 훈련 결과 학습이 잘 진행이 안됨
generator의 성능이 좋지 않아 gradient가 굉장히 작음
gan 훈련 개선 방법
- feature matching
- minibatch discrimination
- historical averaging
- one-sided label smoothing
- virtual batch normalization
- adding noise
- use better metric of dictribution similarity
즉 mode collapsing과 vanishing gradient 문제가 존재하였기 때문에
위 문제들을 해결하기 위해 나온 방법이 WGAN
mode collapsing : 학습시키려는 모형이 실제 데이터의 분포를 모두 커버하지 못하고 다양성을 잃어버리는 현상
//loss만 줄이려하다보니 G가 전체 데이터 분포를 찾지 못하고 한번에 하나의 mode에만 강하게 몰린다.
[GAN : Generative Adverserial Network] 조금 더 구체적으로 설명한 부분
[GAN : Generative Adverserial Network]
game-theoretic 접근 방법
2-player가 있다고 생각하면됨 : 각각 generator과 discriminator
두 네트워크가 서로 적대적 방향의 학습을 진행하며 결론 도출 => 다루기 힘든 밀도함수들의 근사치를 신경 쓸 필요가 사라짐
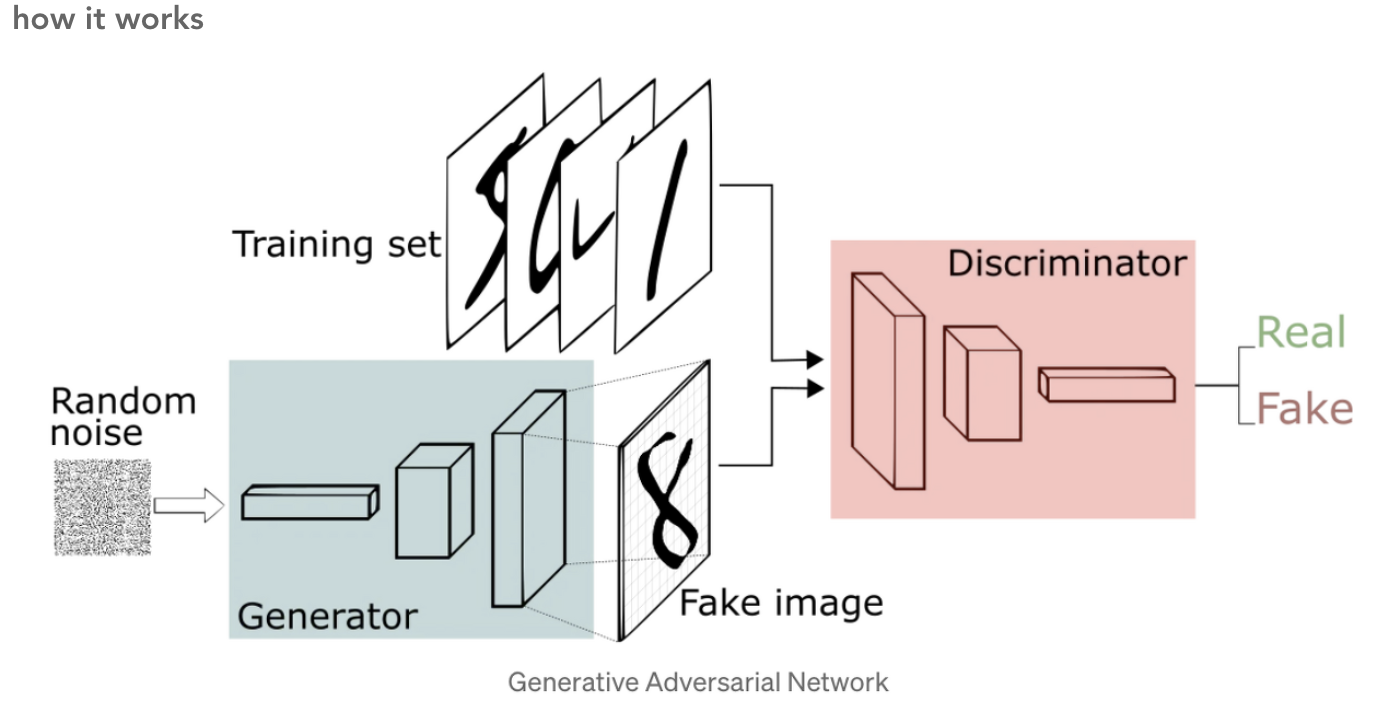
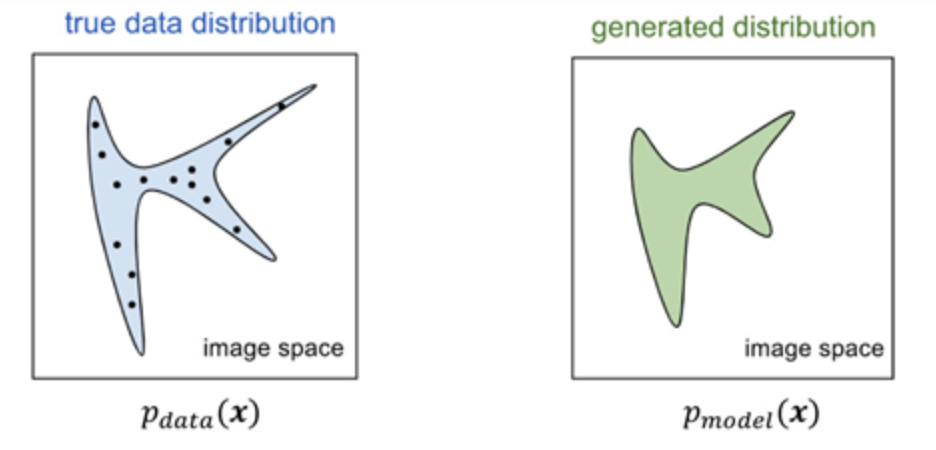
generator의 역할 : true data의 분포와 동일하게 모델이 학습하여 생성해내는 데이터의 분포를 맞춰가는 역할
discriminator의 역할 : generator가 생성해낸 이미지의 real/fake를 가려내는 역할
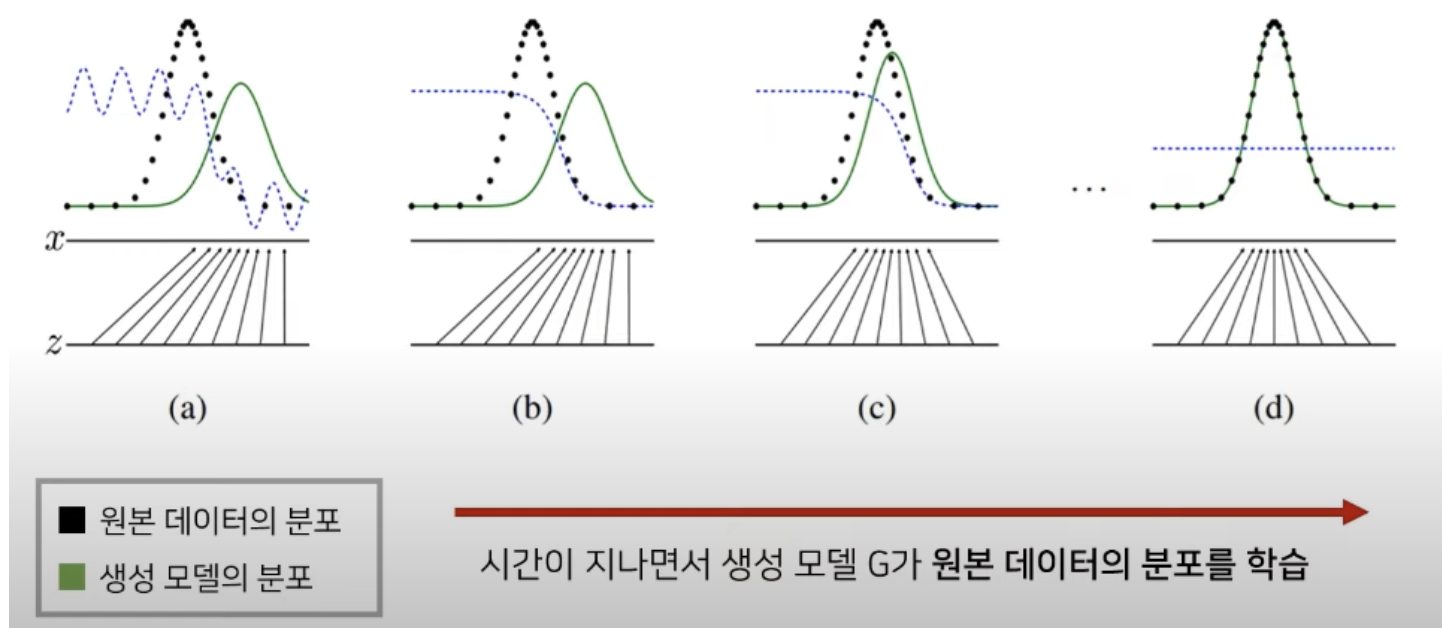

마치 경찰과 위조지폐범과 같다는 비유를 많이 함
generator이 게으르다면 discriminator을 못 속이므로 모델 수렴이 안됨
discriminator이 게으르다면 실제와 구분을 잘 못해 모델 학습이 진행이 안됨

잠깐 minimax algorithm에 대해 알아보자
맛보기 개념) 체스나 바둑, 상대방과 번갈아 하는 게임에 있어서 상대방이 최악의 수를 둔다고 고려하지 않음
상대방이 최선의 플레이를 했을 경우 그 결과가 나에게 최소의 영향을 끼치도록 하는 것이 minimax algorithm
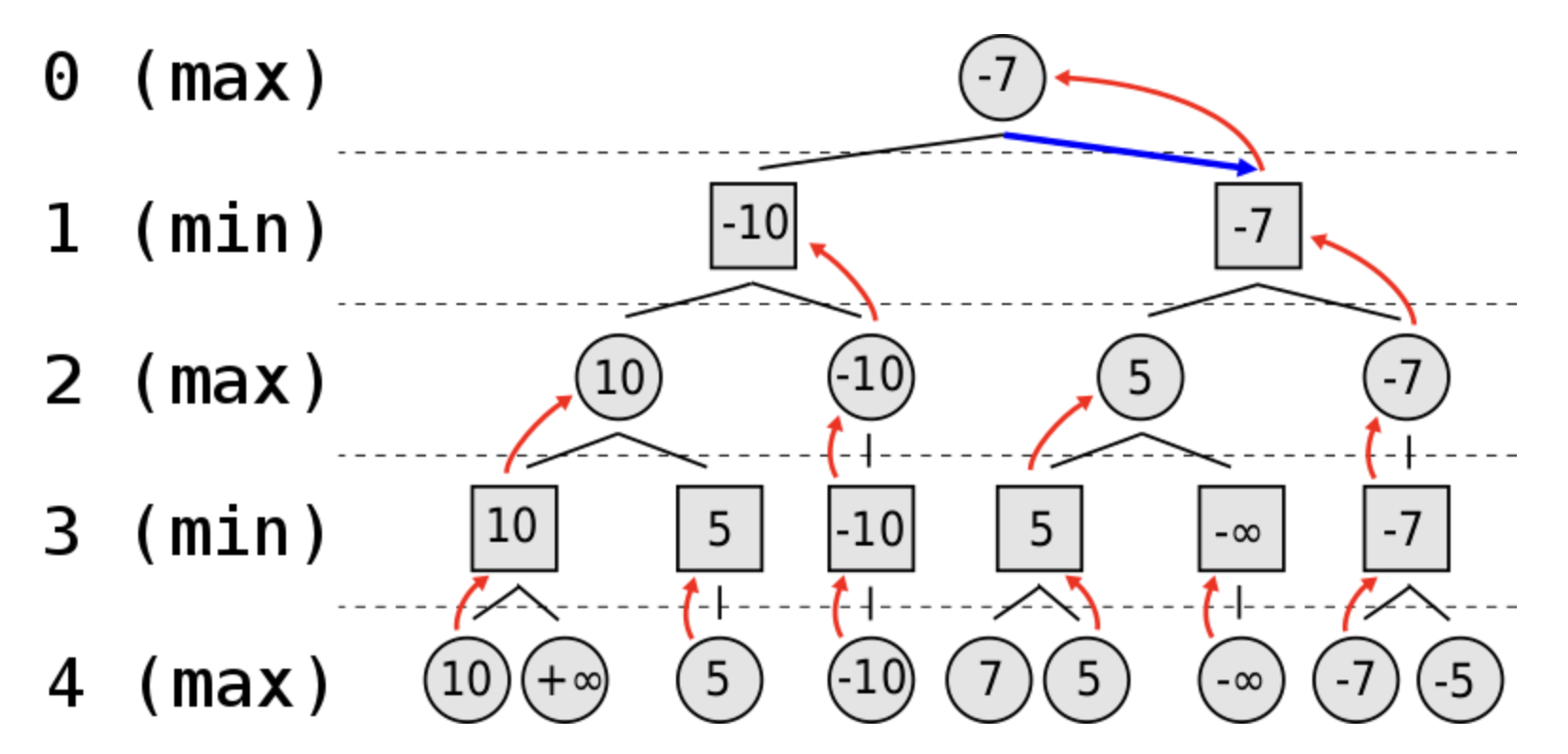
위 그림 ) 4수 앞을 예측한 트리 노드, 0,2,4는 내 차례이므로 max가 되도록, 1,3은 상대방 차례이므로 min이 목적임
다시 GAN으로 돌아가서,, 목적함수를 설명해보겠음

max는 discriminator에 관련된 부분,, 이부분을 하나씩 해석해보자
먼저 Pdata에 대해 discriminator은 최대한 많이 맞춰야한다는 의미,, Dd(x)=1
P(z)에 대해 generator가 생성해낸 데이터들을 discriminator가 true라고 하면 안되므로 이 부분은 1에서 빼 최소가 되도록,,//Dd(Dg(x))=0
그 후 min은 generator에 대한 부분으로 덧셈 앞의 부분은 generator가 영향을 줄 수 없음
+뒷부분에서 generator가 생성해낸 부분이 가장 적어야함
즉 수식 그대로 GAN의 목표를 해석해보자면
1) Pg => Pdata 분포와 동일해지도록해야함
2) D(G(x))가 최종적으로 1/2가 되도록 하는 것 (1/2 = 가짜 이미지와 진짜 이미지 구분 X)
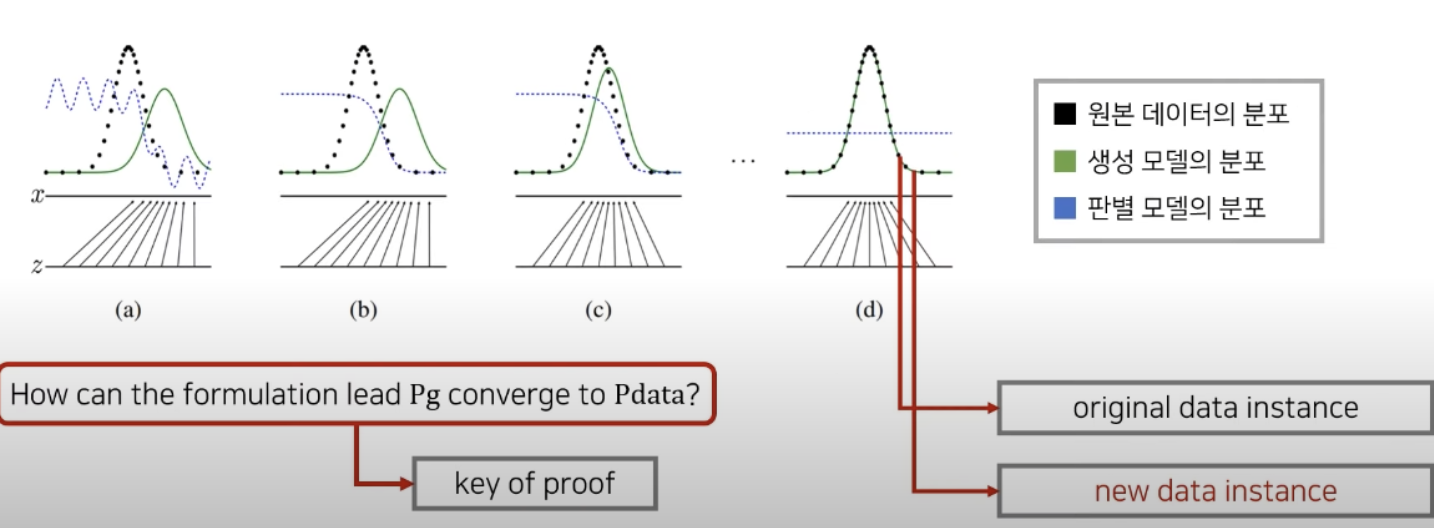
이때 모든 학습이 그렇듯 local optima인지 global optima인지 확인해야함
global optima = 모든 경우에서 최적의 값임
GAN도 문제점이 있음
1) mode collapse
2) vanishing gradient
mode collapse 같은 경우 생성자가 게으른거임.. 생성자가 게을러 판별자가 한 두번 속은 타입의 이미지들만 생성함
= local minimum에 빠지게 됨
vanishing gradient 같은 경우는 생성자의 학습이 판별자의 구분보다 더 어렵나보니 학습을 반복하는 과정에서 모델과 data의 학습이 상이해져 gradient가 0에 다다르게됨 => gradient를 통해 학습을 진행해야하는데 gradient=0이니 제대로된 학습이 진행이 안되는 것임
위 문제들을 해결하기 위해 등장한 것이 WGAN
2) Wasserstein GAN
GAN의 값 함수에서 Jensen-Shannon 발산 대신 연속적인 Wasserstein 거리(=Earth Mover's distance = EM distance) 사용
=> 좀 더 smooth한 측정을 통해 안정적인 gradient descents를 사용한 learning 진행
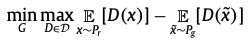
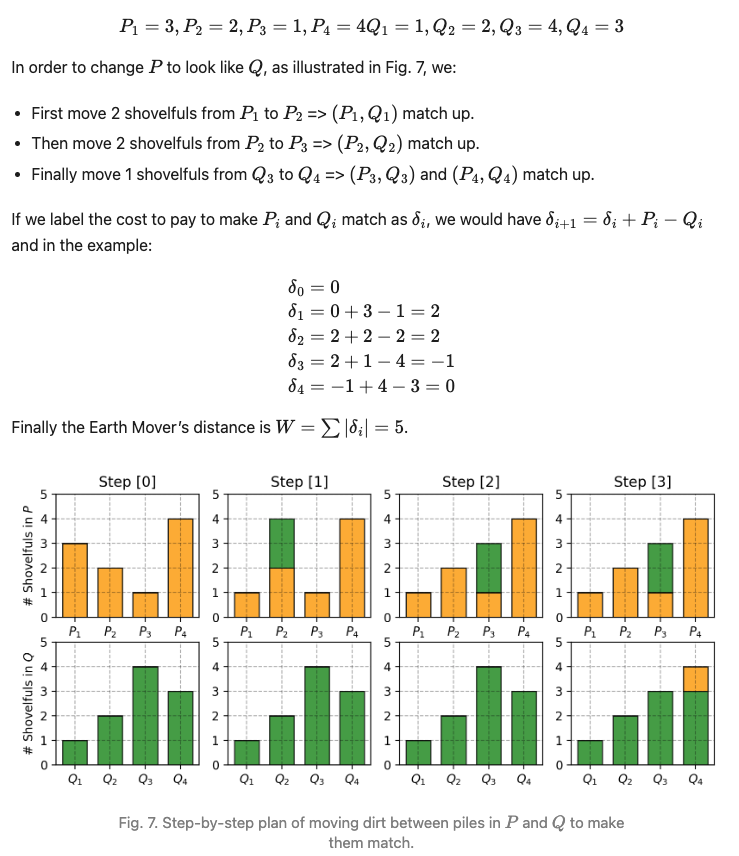
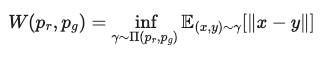
는 에서 로 얼마의 흙 비율이 이동되어야 하는지 설명하여 P가 Q의 확률 분포를 따르도록 만듦
x에 대한 주변 분포는 P로 더해짐
=> P에서 Q로 옮겨진 흙의 총량dr(x,y) * 이동거리c(x,y)
즉 모든 x,y 쌍에 대한 평균 예상 비용 : E(x,y)∼γ[c(x,y)]
위 솔루션 중 최솟값이 EM distance
wgan 조금 더 구체적인 정리
gan 학습은 매우 어렵다.
model은 절대 수렴하지 않고 mode collapses는 흔하다.
앞으로 나아가기 위해 우리는 incremental improvement를 만들거나 새 비용함수를 위한 새로운 path를 수용해야한다.
거리함수가 바뀌면 수렴 방식이 바뀐다
Distance
두 분포 간 유사성/거리 측정 방법
-Kullback-Leibler (KL) Divergence
-Jenson-shannon (JS) Divergence
-Wasserstein 1
KL-Divergence
어떤 분포 p가 다른 분포 q로부터 얼마나 떨어져있는가?
어떤 분포 p가 다른 분포 q의 정보량을 얼마나 잘 보존하는가
=> 정보량을 잘 보존할수록 서로 비슷한 분포
정보이론의 정보량 : 놀람의 정도 (degree of surprise)
h(x)=-logp(x)
정보이론의 엔트로피 : 놀람의 정도의 평균(기대값), 불확실성 정도

p(x) & q(x)가 같으면 0으로 최솟값
p(x)가 0에 가까워지면 q(x)의 효과가 무시됨
분자가 0이면 분모에 상관없이 0으로 비대칭적
이 경우 분포 사이 유사성 측정이 힘들다는 단점
JS-Divergence

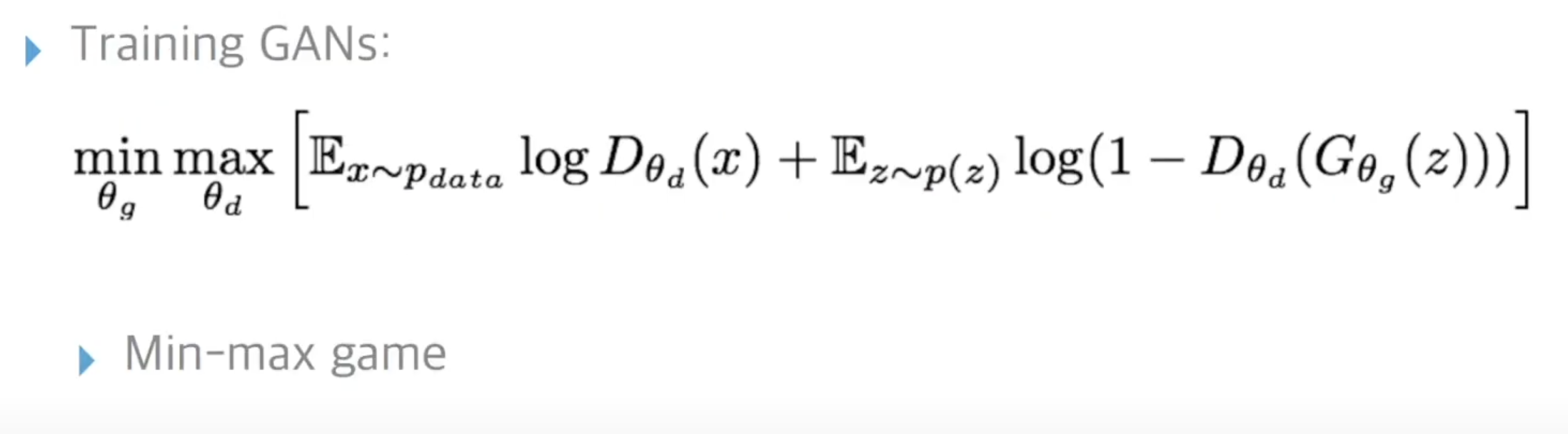
wasserstein distance
두 확률분포간 거리 측정 지표로 Earth Mover's distance(EM distance)라고 불린다.
어떤 확률 분포 모양을 띄는 흙더미를 다른 확률분포 모양을 가지도록 하는데 드는 최소비용
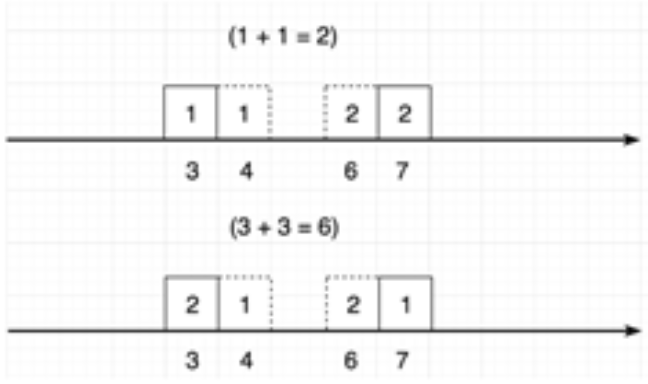
gan과 wgan
-js 발산은 불연속적으로 급격히 변하거나 미분 불가능한 부분 존재
-wasserstein 지표만이 부드러운 측정을 제공하며, 경사하강법을 사용한 안정적인 학습 과정에 유용함
이를 통해 gan의 문제점들을 보완함
근데 이제 wgan을 사용하려면 기반되는 조건이 Lipschitz continuity가 있음
∣f(x)−f(y)∣≤K∣∣x−y∣∣
실수값 함수 f가 모든 x,y에 대해 위 식을 만족할 때 K-Lipschitz 연속
위 조건들이 학습되는 과정
-f가 파라미터 θ로 매개변수화된 1-Lipschitz 연속 함수들이라면
수정된 wasserstein-GAN에서 'discriminator'은 좋은 θ를 찾기 위해 fθ를 학습하는데 사용됨
-손실 함수는 P와 Q 사이 EM distance를 측정하는데 사용됨
위 과정에 따라 discriminator은 더이상 진짜와 가짜를 직접 구별하는 것이 아닌 EM distance를 계산하기 위해 1-Lipschitz 연속함수를 학습하는데 훈련됨
훈련 중 손실함수의 감소에 따라 EM distance는 줄고 생성 모델의 출력은 real data의 분포에 더 근접한다
=> 단, 이때 1-Lipschitz 연속성을 유지해야하는 것이 문제
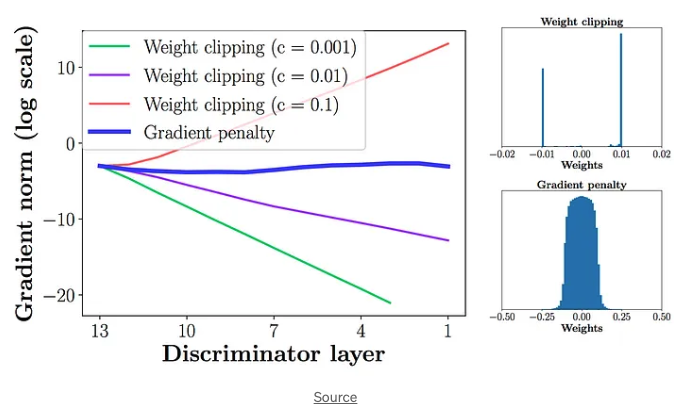
위 조건에 부합하기 위해 트릭 사용
- 가중치 w를 [-0.01,0.01]로 clipping 진행하여 상한과 하한을 얻음 : weight clipping

[Algorithm]
-weight clipping
-wasserstein distance
-Adam => RMSProp 최적화기 사용
3) WGAN-GP


'DL 기본개념' 카테고리의 다른 글
| CV Task (0) | 2023.10.09 |
|---|---|
| [RNN, LSTM, GRU] (1) | 2023.10.02 |
| Generative Adversarial Network란? (0) | 2023.08.01 |
| GAN 학습자료 정리 (0) | 2023.07.27 |
| Data Augmentation (0) | 2023.07.25 |
