https://tkayyoo.tistory.com/134
[Generative] DDPM : Denoising Diffusion Probabilistic Models (NIPS'20)
Paper : https://arxiv.org/abs/2006.11239 Authors Jonathan Ho et al, UC Berkeley, NIPS’20 Main Idea 기존 Diffusion 모델이 High Quality Sample을 Generation할 수 있다는 것을 보임. ε-prediction reverse process parametrization 기법을 제안
tkayyoo.tistory.com
위 티스토리를 참고하여 쓴 글입니다.
베이즈 정리
VAE
VAE의 ELBO
베이즈 정리
conditional distribution
데이터라는 조건이 주어졌을 때의 조건부 확률을 구하는 공식
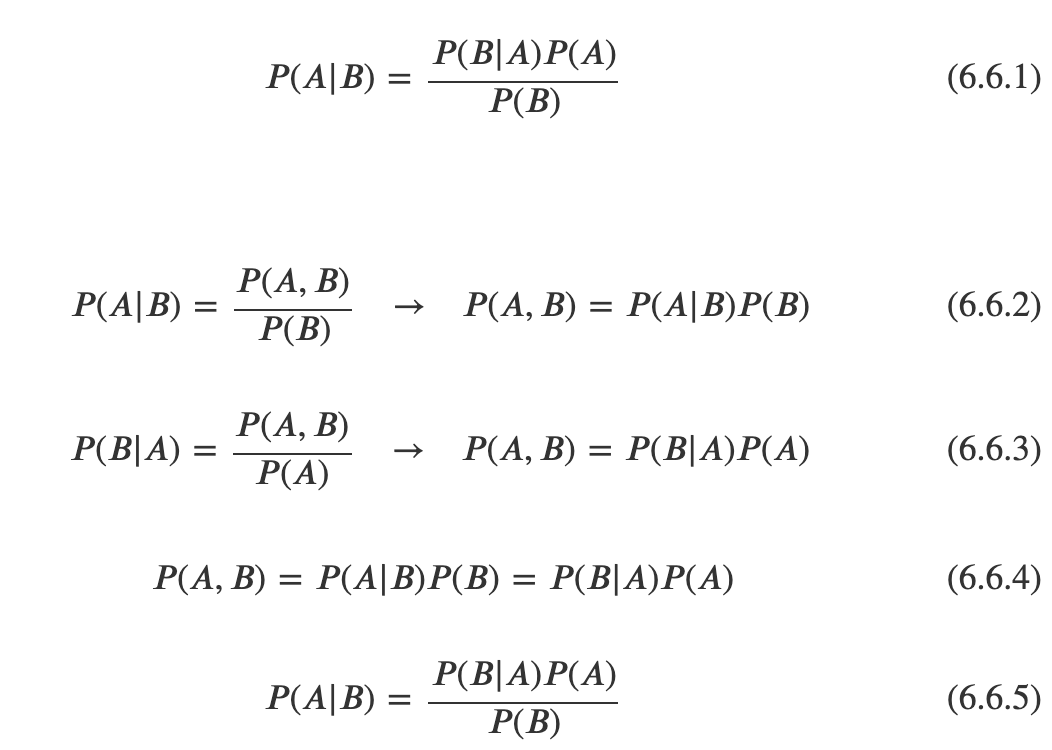
p(A) : 사전 확률(prior) -> 사건 B가 발생하기 전 가지고 있던 A의 확률
p(A|B) : 사후확률(posterior) -> 사건 B가 발생했을 때의 정보를 반영하여 갱신되는 A의 확률
p(B|A) : 가능도(likelihood) -> 사건 A가 발생한 경우 사건 B의 확률
베이즈 정리는 새로운 정보가 기존 추론에 영향을 미치는 것을 보여준다.

위 A, C를 사용하여 식을 전개하면 아래와 같은 결과를 얻을 수 있다.
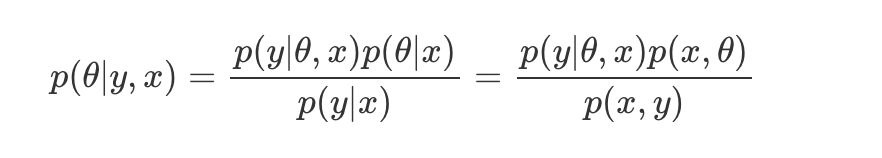
위 식에서 input x와 model parameter θ는 독립임을 이용하여 다시 한 번 아래와 같이 정리 할 수 있다.

θ : 모델 파라미터로 현재의 증거
D : Data로 과거의 경험
x : input
y : output
p(θ|D), p(θ|x,y) : 사후 확률로 이러한 x,y일 때 θ에 대해 궁금해하는 것으로 일반적 DL에서의 우리의 궁극적 목표이다.
p(D|θ), p(y|θ,x) : likelihood로 모델은 θ이고, 인풋은 x인데 이때의 output y를 궁금해하는 것이다
위에서 말했듯이 딥러닝에서의 우리의 목표는 p(θ|D), p(θ|x,y)이다.
하지만 딥러닝에서 최적의 모델인 p(θ)는 알 수 없다.
그렇기 때문에 weight initailization을 적용하여 p(D|θ)를 추론해 가는 것!
데이터 D가 θ 모델을 따를 확률이 최대가 되도록 모델 θ를 찾는것!
위 과정을 MLE:maximun=m likelihood estimation이라 부른다.
하지만 bayesian network라면?
p(θ)를 알 수 있다! => gaussian distribution이라면 모델 확률은 귀납적 반복을 통해 계산 가능
즉, DL의 원래 목표인 p(θ|D), p(θ|x,y)를 구할 수 있고 이를 직접 최대화하는 방향으로 학습을 진행하게 된다.
위 방법이 MAP:maximun a posteriori이다
MAP와 MLE
MAP는 모델의 확률을 알 수 있기 때문에 모델의 확률을 고려하며 likelihood의 max를 찾는 것이며 MLE는 MAP와 동일하지만 모델의 확률을 모르는 상태에서의 likelihood의 max를 찾는 과정을 말한다.
VAE
Variational AutoEncoder

가정 : 모든 분포는 gaussian distribution이다
- gaussian encoder : input Xi에 대한 Zi의 평균과 분산 계산함
- Zi : latent space로 Zi의 평균과 분산이라 함은 latent space의 True 분포를 의미한다
- Zi는 decoder를 통과하여 output을 생성한다
- Zi -> sampling -> output1, output2...
- 이때 samplig은 random process이기 때문에 일반적 네트워크처럼 back propagation을 통해 적용할 수 없음
- reparametrization trick : 따로 sampling을 적용하여 평균과 분산에 반영해준다
이때, VAE를 떠올리면 AE 또한 생각나는데 이 둘의 차이를 알아보자면
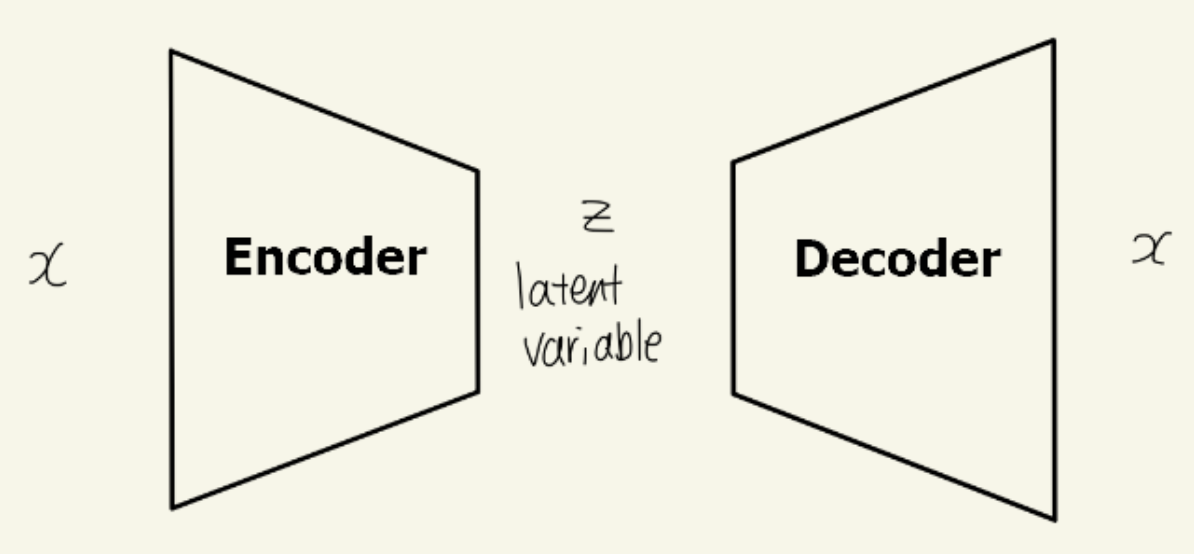
둘 다 오토인코더 구조이지만 AE는 encoder를 알아내는 것이 목표, 즉 input data의 feature를 가장 잘 표현하는 manifold를 찾는 것이 목표이며 VAE는 decoder에 집중하여 그에 맞는 output을 도출하는 것이 목적이다.
+ Auto Regressive(AR)는 과거 움직임을 기반으로 미래를 예측하는 것으로 주로 시계열 데이터에 자주 이용된다
여기서의 auto는 자기 자신을 의미한다고 보면 이해하기 더 쉬울 것이다.
VAE의 ELBO
VAE 모델을 학습하려면 어떠한 loss function 혹은 objective function을 사용해야할까?
-> decoder를 학습하는 것이 목표, 즉, p(θ)의 maximum을 구하는 것이 목표!
p_θ(x|z) : input x와 동일한 x가 decoder로부터 나올 확률
다시 말해 input x의 분포가 잘 나올 확률 p(x)를 최대화하는 것이 최종 목적이다
p(x)의 objective function을 풀어나가보면 posterior인 p_θ(x|z)를 구해야 우리가 원하는 결과를 알 수 있음
하지만 posterior distribution의 경우, closed form이 아니기 때문에 매우 intractable함
-> 무수히 많은 z에 대해 모두 계산하는 것은 쉽지 않음
따라서 우리가 알기 쉬운 분포인 encoder의 분포를 도입하여 문제를 해결하게 됨
-> 구하기 어려운 분포를 다루기 쉬운 확률 분포로 근사하는 방법 : variational inference (VI)
VI : 변분추론
상수, 변수, 일반적 연산이나 함수 등으로 표현 가능한 closed form이 아니거나 굉장히 난해한 경우, 다루기 어려운 분포를 최소화하기 위해 이상적 다른 분포를 가정하여 근사해 해결하게 됨
- Monte Carlo Sampling
어떠한 분포를 가정하고 여러번 샘플링하여 평균을 구한다.
여러번 샘플링하여 구한 본 '평균과 전체에 대한 기댓값이 같아질 것'
- Stochastic Variational Inference : SVI
KLD를 줄이는 쪽으로 파라미터를 업데이터하는 방법
stochastic gradient descent를 활용함
단, KLD가 미분 가능해야한다.
- Variation EM algorithm
posterior p_θ(x|z)를 알기 위해 미지의 파라미터들을 동시에 알아내는 것을 포기하고
expectation과 maximization을 활용하는 방법
- expectation : monte carlo 방법등을 활용하여 파라미터 도출
추가적 용어
Monte Carlo Approximation
넓이 1인 직사각형에 걸쳐진 1/4 원 넓이를 구해보자!
직사각형 환경에 무작위로 수많은 점을 찍는다
'충분히 많은 점들이 찍혔을 때의 원 안으 점 개수와 전체 점 개수 비율로 넓이를 구해주면 정답에 근사한다'
=> 즉 무수히 많은 시도를 해보면, 정답을 알 수 있다.
위의 예시는 매우 쉬운 예제이지만 아주 복잡한 문제를 풀고자 할 때 용이하다.
KL-divergence
kullback-leibler divergence
두 확률분포의 차이를 계산하는데 사용되는 함수
그 분포를 근사하는 다른 분포를 사용해 샘플링하고 발생할 수 있는 엔트로피 차이를 계산한다
말 그대로 '두 분포의 차이'
- 0 이상이다 = non-negative
cross-entropy - entropy이며 cross-entropy의 lower bound는 entropy임
- 거리 개념이 아니다
KL(p||q) != KL(q||p)
=> 추후에 cross entropy 공부해서 더 자세하게 정리해두겠음
https://hyunw.kim/blog/2017/10/27/KL_divergence.html
초보를 위한 정보이론 안내서 - KL divergence 쉽게 보기
사실 KL divergence는 전혀 낯선 개념이 아니라 우리가 알고 있는 내용에 이미 들어있는 개념입니다. 두 확률분포 간의 차이를 나타내는 개념인 KL divergence가 어디서 나온 것인지 먼저 파악하고, 이
hyunw.kim
ELBO : evidence of lower bound
KLD는 0 이상이다라는 조건을 사용해 찾아낸 lowewr bound
- ELBO는 Lower bound -> 이를 최대화한다면 objective function을 최대화한다고 볼 수 있다

=> ELBO도 마찬가지
'DL 기본개념' 카테고리의 다른 글
| Transformer outline (0) | 2025.03.27 |
|---|---|
| Deep Learning : ANN, DNN, RNN, CNN (SLP, MLP) (1) | 2024.03.07 |
| Wavenet 논문 전체 내용 (1) | 2023.11.01 |
| Object Detection 개념 정리 및 학습일지 (0) | 2023.10.27 |
| CV Task (0) | 2023.10.09 |



