머신러닝 (machine learning : ML)
주어진 입력 데이터를 통해 답을 유추해주는 최적의 함수를 찾는 것
: 각 머싱러닝 기법에 따라 최적의 함수를 찾는 기법이 다름
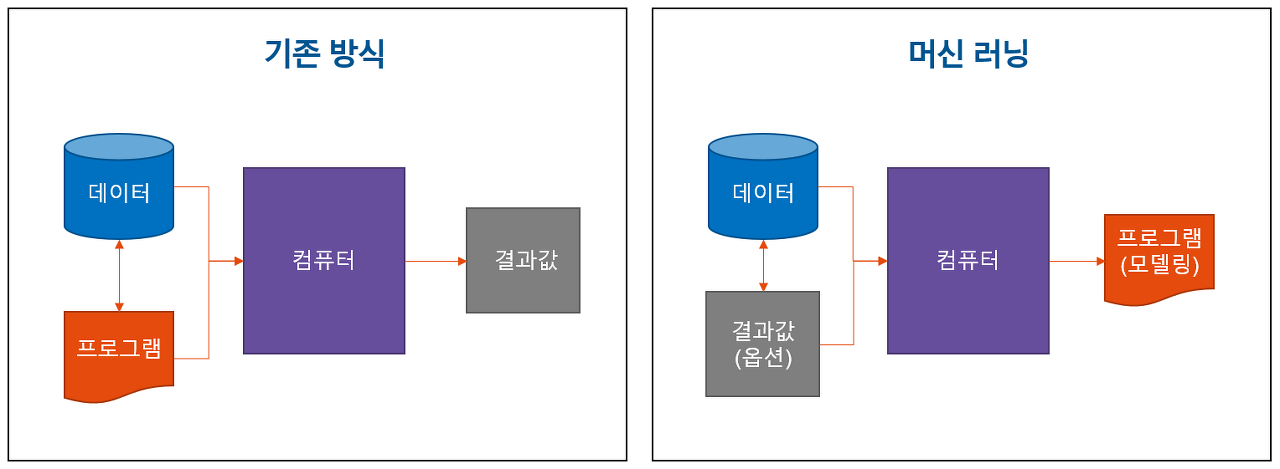
복잡한 문제 => 데이터 기반으로 패턴 인지, 해결 //예측 오류 최소화하는 최적화 알고리즘을 통해 학습
머신러닝 중 딥러닝
: 인간 뇌의 학습과 메커니즘 모방

neuron : 임계치 이상의 자극 => 다른 뉴런으로 자극 전달 //딥러닝도 마찬가지
: F(x)=w0 + w1*x1 + w2*x2 ... + wn*xn //x = 입력값
=> 딥러닝은 최적의 가중치 w값을 학습을 통해 도출
즉, 딥러닝은 가중치 w값을 학습함 //최적의 파라미터 도출
2012 : AlexNet
2014 : VGG
2014 : GoogLeNet
2015 : ResNet
딥러닝 장점
- 유연하고 확장성 있는 모델 구성 //CNN-feature extractor(!= feature engineering), 최적화 어려운 문제들 모델링 수행
-다양한 영역에서 확장되어 활용 //영상, 음성, 자연어 등 다양한 영역 최적화 문제 해결책 제시
퍼셉트론 (perceptron)
: 초기 인공 신경망 //가장 단순한 형태
다수의 신호를 입력받아 하나의 신호를 출력
hidden layer, single layer로만 구성
입력 피처들과 가중치, activcation, 출력 값으로 구성

-weighted sum : 입력 피처들의 개별 값과 각각의 가중치를 곱한 값들을 더해서 최종적으로 나온 값
-activation function : 입력 신호의 총합을 출력신호로 변화하는 함수 //계단 함수 (step function)
이러한 step function 이외 함수를 사용하면 신경망에서 자주 사용하는 활성화 함수로 sigmoid function이 있음
=> 둘의 차이는 '매끄러움' => 시그모이드 함수는 부드러운 곡선임, 입력에 따라 출력이 연속적으로 변화함
계단 함수는 0 or 1 하나의 값만 돌려줌
-출력 값 : F(입력값의 weighted sum)
=> 퍼셉트론의 학습 과정 : 학습 결과인 예측값과 실제값과의 차이가 최소가 되는 weight 값을 찾는 과정
= 그렇다면 예측값과 실제값의 차이로 어떻게 최소 weight 값을 얻느냐? : 경사하강법 사용
= 회귀를 통해 구체적으로 알아보자
회귀(regression)
-머신러닝에서의 회귀 예측의 핵심 : 주어진 피처와 결정 값 데이터 기반 학습으로 최적의 회귀 계수 찾는 것
"오류 값 합이 최소가 되는 계수"
= 전체 데이터의 잔차 합이 최소가 되는 모델 형성
-오류 값 측정 방법
1) RSS (residual sum of square)
: 오류 값의 제곱을 구해서 더함 //오류 값은 양수와 음수가 있으므로 둘이 상쇄될 수 있기 때문에
Error^2 = RSS
여전히 우리의 중심 변수는 w임 // w = 가중치
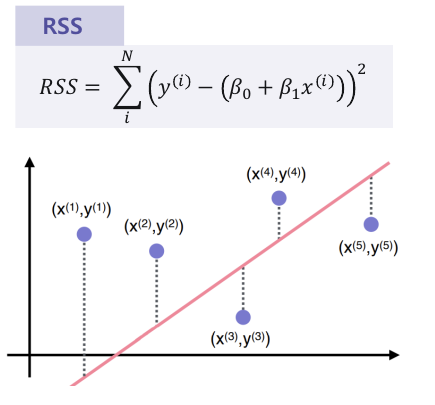
단순 오차
가장 간단, 직관적
오차를 그대로 이용해 입력 값 크기에 의존적
절대적인 값 비교는 힘듦
2) MSE (mean square error)
RSS를 데이터수로 나눔

이상치(outlier)에 민감
직관적 해석 가능
마찬가지로 절대적 값은 비교가 안됨
= 회귀에서 mse는 cost임
즉, w 변수로 구성되는 mse는 비용함수(loss function, object function)임
머신러닝 회귀 알고리즘은 데이터를 반복 학습하며 비용함수 반환 값을 감소시킴
최종적으로는 더 이상 감소하지 않는 최소의 오류값을 구하는 것이 목표
일반적, w 파라미터가 굉장히 많음
= 이러한 고차원 방정식에 대한 문제 해결해주면서 비용 함수 rss를 최소화해주는 방법이 경사 하강법임
경사하강법 (Gradient Descent)
: 점진적인 하강
점진적, 반복적 계산을 통해 w 파라미터 값 update해 오류값이 최소가 되는 w 파라미터 도출
how?
미분을 통해 비용함수의 최소값 찾음
미분 - 증가, 감소의 방향성을 나타냄 //미분된 1차 함수 기울기가 최소인 점 = 비용함수가 최소인 지점
1) 손실함수의 각 w값을 각각 편미분
2) 편미분 값에 학습률을 곱해 감소시킴 : 편미분 값 update
위 과정을 정해진 iteration만큼 반
'DL 기본개념' 카테고리의 다른 글
| [RNN, LSTM, GRU] (1) | 2023.10.02 |
|---|---|
| GAN, WGAN, WGAN-GP (0) | 2023.09.19 |
| Generative Adversarial Network란? (0) | 2023.08.01 |
| GAN 학습자료 정리 (0) | 2023.07.27 |
| Data Augmentation (0) | 2023.07.25 |
