Generative Adversarial Nets

adversarial process를 통한 생성형 모델의 새로운 측정 프레임워크를 제안

데이터의 분포를 학습하는 generative model G와 생성된 데이터샘플의 확률을 측정하는 discriminative model D

 

Adversarial인 이유 : G는 D가 mistake을 많이 하도록 확률을 학습하기 때문

                                                Minimax two-player framework

 

이상점은 G가 훈련 데이터의 분포를 잘 학습했고 여기서 D의 T/F 판별 확률이 1/2인 것이다.

이 점이 더 이상 개선을 할 것이 없는 유일한 해가 된다

 

G와 D가 다층 퍼셉트론(MLP, Multilayer Perceptron)으로 정의되는 경우, 시스템 전체는 역전파(backpropagation) 알고리즘을 통해 훈련될 수 있다 이를 통해 복잡한 Markov chain 등을 사용할 필요 없이 MLPs를 사용해 G와 D 모두 학습 가능하다!!

---

 

딥러닝의 생성 분야의 문제점

• 최대 우도 추정과 관련된 복잡한 확률적 계산을 근사하는 데 어려움 존재
• 생성적 맥락에서 조각별 선형 유닛의 이점을 활용하는 데 한계가 있음

 

따라서 Adverserial framework를 사용하여 본 문제점을 해결하고자 하였다

: Backpropagation & Dropout 만을 사용

: 생성의 경우에는 forward propagation만 사용

 

G:Generative model은 위조 지폐를 생성하는 위조자, D:Discriminator model은 이를 판별하고자 하는 경찰로 비유

 

Adversarial Nets

모델이 모두 MLPs일 때 가장 간단하게 적용할 수 있다

 

생성자 분포 Pg

입력 노이즈 변수에 대한 사전확률 Pz(Z) - 일반적으로 정규 분포 사용

MLPs의 매개변수 θg - 그 중 생성자 네트워크 G의 매개변수

생성형 모델의 데이터 공간 매핑 확률 G(z;θg​) - z를 입력받아 실제 데이터 공간 샘플 x로 매핑하여 생성자가 노이즈를 실제 데이터로 변환​

두 번째 다층 퍼셉트론 D(x;θd​) - D(x)는 x가 생성된 데이터 Pg가 아닌 실제 원본 데이터로부터 왔을 확률

 

 

정리해보자면,

생성자 G : 입력 노이즈 z를 받아 실제와 유사한 데이터 샘플 G(z; θg) 생성

판별자 D : 입력된 데이터 x가 실제 데이터 Pdata(x)인지 생성자로부터 생성된 Pg(x)인지 D(x; θd) 출력

 

학습 과정은 D는 올바른 레이블 할당 확률 최대화, G는 log(1-D(G(z)))를 최소화해 D가 생성된 데이터를 오인하도록 만듦

 

 

 

 실제 데이터 x가 D에 의해 True로 분류될 확률 로그의 평균 -> 즉 D의 True data 구분 훈련시키는 항

: 실제 데이터 분포인 Pdata에서 샘플링된 x에 대해 D가 x를 실제라고 분류할 확률을 나타내는 항

 

생성자 G가 생성한 가짜 데이터 G(z)가 판별자 D에 의해 False라고 분류될 확률의 로그 평균 -> 즉, 생성자를 통해 생성된 데이터를 False라 판별할 수 있도록 D를 훈련시키는 항

 

=> D model은 minimax의 두 항을 최대화 하여 실제 데이터는 T로, 생성된 데이터는 F로 분류하도록 학습한다

=> G model은 log(1-D(G(z)))를 최소화하고자 한다

 

 

Theoretical Results

생성자는 노이즈 z를 입력받아 데이터 공간에 매핑함으로써 확률분포 Pg를 정의한다

이때 알고리즘 1이 충분한 용량과 훈련시간을 갖춘다면 Pg가 실제 데이터 분포인 Pdata를 잘 추정하기를 기대한다

a. 생성 분포가 실제 데이터 분포와 유사해지며 d는 부분적으로 정확함 / b. 알고리즘 내부 루프에서 판별자 D는 두 분포를 구분하도록 훈련됨 / c. 판별자 D의 기울기가 생성자에게 G(z)를 실제 데이터로 분류될 가능성이 높은 영역으로 유도하여 생성 데이터의 질이 향상된다. / d. 여러 roof를 거치며 G와 D가 충분한 용량을 가지게 되면 두 분포를 구분할 수 없게 된다.

 

[ 실제 데이터 샘플과 노이즈 샘플을 샘플링하여 가짜 데이터 G(z)를 생성 -> D의 손실함수 계산 및 최소화 -> 새로운 노이즈 샘플 z샘플링하여 가짜 데이터를 다시 생성하여 생성자 손실함수 update ] 반복

 

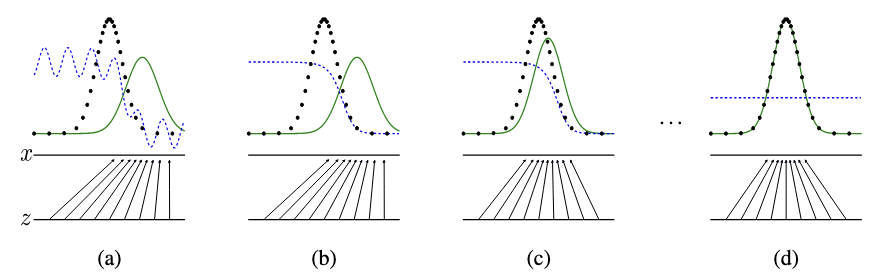
=> 이 과정에서 일반적으로 판별자를 K번 업데이트 한 후 이가 끝나면 생성자를 업데이트 한다

이는 판별자가 생성자에 비해 항상 상대적으로 더 최적화되도록 유지하기 위함이다.

minimax game의 형태이자 서로 적대적 관계인 두 네트워크를 학습시키는 만큼 두 네트워크 간의 균형 유지가 중요하다

여기서 판별자를 생성자 보다 더 여러 번 update하는 이유는 판별자가 더 강해야 생성자가 더 정교한 데이터를 생성해낼 동기가 생기기 때문이다. 더불어 생성자의 효과적 학습을 위해서는 판별자의 정확한 피드백이 존재해야하기 때문이다. 

하지만 이 과정에서 판별자가 지나치게 잘 학습이 되면 생성자는 유용한 기울기를 받기 어려워져 판별자 또한 적절한 업데이트를 통해 과적합을 방지하며 생성자에게 균형잡힌 피드백을 제공해야한다.

 

 

Experiments

 

• 훈련 데이터셋:
  • MNIST: 손글씨 숫자 데이터셋.
  • Toronto Face Database (TFD): 얼굴 이미지 데이터셋.
  • CIFAR-10: 10개의 클래스에 속하는 컬러 이미지 데이터셋.
• 네트워크 아키텍처:
  • 생성자 네트워크 (Generator Nets):
    • 활성화 함수: 렉티파이어 선형 활성화(ReLU)와 시그모이드 활성화의 혼합.
    • 노이즈 입력: 생성자의 가장 하위 층에만 노이즈 적용.
  • 판별자 네트워크 (Discriminator Net):
    • 활성화 함수: 맥스아웃 활성화(maxout).
    • 드롭아웃: 판별자 네트워크 훈련 시 드롭아웃 적용.
• 로그-우도 추정 방법:
  • Gaussian Parzen Window: 생성자 GGG로 생성된 샘플에 Gaussian Parzen 윈도우를 적합시켜 테스트 세트 데이터의 확률을 추정.
  • σ\sigmaσ 파라미터: 검증 세트를 사용하여 교차 검증을 통해 결정.

 

 

 

Advantages and Disadvantages

1. 단점 (Disadvantages)

• 명시적인 pg(x)p_g(x)pg​(x) 표현의 부재:
  • GAN에서는 생성자 GGG가 pg(x)p_g(x)pg​(x)를 암묵적으로 정의하지만, 이를 명시적으로 표현하지 않습니다. 이는 pg(x)p_g(x)pg​(x)의 직접적인 분석이나 해석이 어려울 수 있음을 의미합니다.
• 판별자 DDD와 생성자 GGG의 동기화 필요성:
  • 훈련 과정에서 DDD와 GGG가 잘 동기화되어야 합니다. 특히, DDD를 충분히 업데이트하지 않고 GGG를 과도하게 훈련시키면 "Helvetica 시나리오"가 발생할 수 있습니다.
  • Helvetica 시나리오: GGG가 너무 많은 zzz 값을 동일한 xxx 값으로 수렴시켜, 생성된 데이터의 다양성이 부족해지는 상황을 말합니다. 이는 GAN의 훈련이 제대로 이루어지지 않게 만들며, pgp_gpg​가 pdatap_{\text{data}}pdata​를 충분히 모델링하지 못하게 합니다.
  • 비유: 이는 볼츠만 머신에서 네거티브 체인이 학습 단계 사이에 최신 상태로 유지되어야 하는 것과 유사합니다. 두 모델 간의 균형을 유지하는 것이 중요합니다.

2. 장점 (Advantages)

• 마르코프 체인의 불필요성:
  • GAN은 마르코프 체인을 사용하지 않기 때문에, 모델의 복잡성이 낮아지고 계산 비용이 줄어듭니다.
• 오직 역전파(backpropagation)만 사용:
  • 그래디언트를 얻기 위해 오직 역전파 알고리즘만 사용되므로, 학습 과정이 단순해집니다.
• 학습 중 추론(inference)이 필요 없음:
  • GAN은 학습 중에 명시적인 추론 단계를 필요로 하지 않아, 학습 과정이 더 효율적입니다.
• 다양한 함수의 통합 가능성:
  • GAN은 다양한 활성화 함수나 네트워크 구조를 모델에 쉽게 통합할 수 있어, 유연성이 높습니다.

3. 추가적인 장점 (Additional Advantages)

• 통계적 장점:
  • 생성자 네트워크가 데이터 예제와 직접적으로 업데이트되지 않고, 판별자를 통과하는 그래디언트만을 통해 업데이트되기 때문에, 입력의 구성 요소가 생성자의 매개변수로 직접 복사되지 않습니다. 이는 데이터의 복잡한 특성을 더 잘 학습할 수 있게 합니다.
• 날카롭고 퇴화된 분포의 표현:
  • GAN은 매우 날카롭고 퇴화된 분포를 표현할 수 있습니다. 반면, 마르코프 체인을 기반으로 한 방법들은 체인이 모드 간에 원활하게 혼합될 수 있도록 분포가 다소 흐릿해야 하는 제한이 있습니다. 이는 GAN이 복잡한 데이터 분포를 더 정밀하게 모델링할 수 있게 합니다.

4. 표 2: GAN과 다른 생성 모델들의 비교

• Parzen window 기반 로그-우도 추정치:
  • 다양한 생성 모델들의 성능을 비교한 표로, GAN이 다른 모델들에 비해 높은 로그-우도 점수를 기록하고 있음을 보여줍니다. 이는 GAN이 더 정교한 데이터를 생성할 수 있음을 시사합니다.

5. 실험적 관찰과 이론적 한계

• 계산적 장점:
  • GAN의 주요 장점은 계산적 효율성에 있습니다. 이는 마르코프 체인이나 다른 복잡한 방법들을 사용하지 않음으로써 얻어집니다.
• 통계적 장점:
  • 생성자가 직접적으로 데이터 예제와 업데이트되지 않기 때문에, 더 일반화된 특성을 학습할 수 있습니다.
• 표현력:
  • GAN은 매우 복잡하고 날카로운 분포를 모델링할 수 있어, 다양한 데이터 유형에 적용하기 적합합니다.
• 이론적 한계:
  • GAN의 단점 중 하나는 pg(x)p_g(x)pg​(x)의 명시적 표현이 없다는 점과, DDD와 GGG의 동기화가 필요하다는 점입니다. 이는 이론적인 보장이 부족한 실용적인 문제를 야기할 수 있습니다.